
【题目】已知几何体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 面
面![]() ,
,![]() ,
,![]() .
.
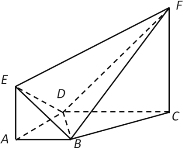
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角E-BD-F的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由勾股定理逆定理证得![]() ,再由已知得
,再由已知得![]() 平面
平面![]() ,
,![]() ,从而有线面垂直,得面面垂直;
,从而有线面垂直,得面面垂直;
(2)分别以DA、DC所在直线为![]() 轴、
轴、![]() 轴,以D为垂足作面DAC的垂线DZ为
轴,以D为垂足作面DAC的垂线DZ为![]() 轴,建系,写出各点坐标,求出二面角两个面的法向量,由法向量夹角的余弦值得二面角的余弦值(注意判断二面角是锐角还是钝角).
轴,建系,写出各点坐标,求出二面角两个面的法向量,由法向量夹角的余弦值得二面角的余弦值(注意判断二面角是锐角还是钝角).
(1)证明:在直角梯形![]() 中由已知可得
中由已知可得![]()
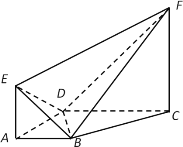
![]()
![]() ,且
,且![]() 面
面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 面
面![]() ,
,![]() ,
,
![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]()
∴![]() 面
面![]()
且![]() 面
面![]() ,故面
,故面![]() 面
面![]() ;
;
(2)分别以DA、DC所在直线为![]() 轴、
轴、![]() 轴,以D为垂足作面DAC的垂线DZ为
轴,以D为垂足作面DAC的垂线DZ为![]() 轴,建系如图
轴,建系如图
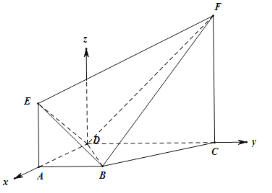
![]() ,
,
则![]() ,
,
设面DEB的法向量为![]() ,
,
则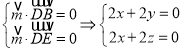 ,
,
取![]() ,则
,则![]() ,故
,故![]()
设面DBF的法向量为![]() ,则
,则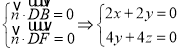 ,
,
取![]() ,则
,则![]() ,故
,故![]()
则![]() ,
,
由图可得二面角E-BD-F的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过动点![]() 且平行于
且平行于![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求动点
,求动点![]() 到直线
到直线![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时至21世纪.环境污染已经成为世界各国面临的一大难题,其中大气污染是目前城市急需应对的一项课题.某市号召市民尽量减少开车出行以绿色低碳的出行方式支持节能减排.原来天天开车上班的王先生积极响应政府号召,准备每天从骑自行车和开小车两种出行方式中随机选择一种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛掷6枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于4,则该天出行方式与前一天相同,否则选择另一种出行方式.
(1)求王先生前三天骑自行车上班的天数X的分布列;
(2)由条件概率我们可以得到概率论中一个很重要公式——全概率公式.其特殊情况如下:如果事件![]() 相互对立并且
相互对立并且![]() ,则对任一事件B有
,则对任一事件B有![]() .设
.设![]() 表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
①用![]() 表示
表示![]() ;
;
②王先生的这种选择随机选择出行方式有没有积极响应该市政府的号召,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车制造厂制造了某款汽车.为了了解汽车的使用情况,通过问卷的形式,随机对50名客户对该款汽车的喜爱情况进行调查,如图1是汽车使用年限的调查频率分布直方图,如表2是该50名客户对汽车的喜爱情况.
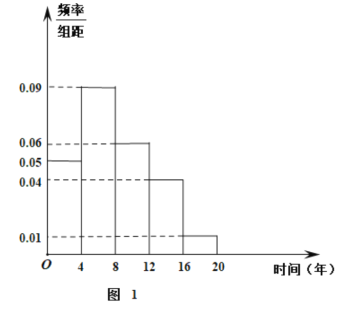
表2
不喜欢该款汽车 | 喜欢该款汽车 | 总计 | |
女士 | 11 | ||
男士 | 23 | 30 | |
总计 |
(1)将表2补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢该款汽车与性别有关;
(2)根据图中的数据,甲说:“中位数在![]() 组内”;乙说:“平均数大于中位数”;丙说:“中位数和平均数一样”,针对三位同学的说法,你认为哪种说法合理,给出说明.
组内”;乙说:“平均数大于中位数”;丙说:“中位数和平均数一样”,针对三位同学的说法,你认为哪种说法合理,给出说明.
附:![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次![]() 普查,为此需要抽验1000人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
普查,为此需要抽验1000人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案①:将每个人的血分别化验,这时需要验1000次.
方案②:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血只需检验一次(这时认为每个人的血化验
个人的血只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这样,该组
个人的血样再分别进行一次化验,这样,该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案②中,某组![]() 个人的每个人的血化验次数为
个人的每个人的血化验次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)设![]() ,试比较方案②中,
,试比较方案②中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】向量集合![]() ,对于任意
,对于任意![]() ,以及任意
,以及任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“
为“![]() 类集”,现有四个命题:
类集”,现有四个命题:
①若![]() 为“
为“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
②若![]() ,
,![]() 都是“
都是“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
③若![]() 都是“
都是“![]() 类集”,则
类集”,则![]() 也是“
也是“![]() 类集”;
类集”;
④若![]() 都是“
都是“![]() 类集”,且交集非空,则
类集”,且交集非空,则![]() 也是“
也是“![]() 类集”.
类集”.
其中正确的命题有________(填所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com