
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)设函数![]() ,
, ![]() ,
, ![]() 为自然对数的底数.当
为自然对数的底数.当![]() 时,若
时,若![]() ,
, ![]() ,不等式
,不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
【答案】(1)单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)3
;(2)3
【解析】试题分析:(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题等价于等价于, ![]() 对
对![]() 恒成立,,设
恒成立,,设![]() ,求出函数的导数,根据函数的单调性求出k的最大值即可.
,求出函数的导数,根据函数的单调性求出k的最大值即可.
试题解析:(1)对函数求导得![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 单调递增,
单调递增,
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)当![]() 时,由(1)可知
时,由(1)可知![]() ,
,
![]() ,
, ![]() ,不等式
,不等式![]() 成立等价于当
成立等价于当![]() 时,
时, ![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
因为![]() 时
时![]() ,
,
所以![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
设![]() ,
,
则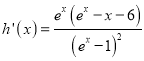 ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
而![]() ,
, ![]() ,
,
所以![]() ,
,
所以存在唯一的![]() ,使得
,使得![]() ,即
,即![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,所以函数
,所以函数![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() ,所以函数
,所以函数![]() 单调递增,
单调递增,
所以当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() ,同时也为最小值,
,同时也为最小值,
因为![]()
![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 的最大整数值是
的最大整数值是![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() 所示,一条直角走廊宽为
所示,一条直角走廊宽为![]() ,
,![]()


(1)若位于水平地面上的一根铁棒在此直角走廊内,且![]() ,试求铁棒的长
,试求铁棒的长![]() ;
;
(2)若一根铁棒能水平地通过此直角走廊,求此铁棒的最大长度;
(3)现有一辆转动灵活的平板车,其平板面是矩形,它的宽![]() 为
为![]()
![]() 如图2.平板车若想顺利通过直角走廊,其长度
如图2.平板车若想顺利通过直角走廊,其长度![]() 不能超过多少米?
不能超过多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)+![]() (a∈R).
(a∈R).
(1)当a=1时,求函数f(x)在点(0,f(0))处的切线方程;
(2)讨论函数f(x)的极值;
(3)求证:ln(n+1)> ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是等差数列,a1=f(x+1),a2=0,a3=f(x-1),其中f(x)=x2-4x+2.
(1)求通项公式an;
(2)若数列{an}为递增数列,令bn=an+1+an+2+an+3+an+4,求数列{![]() }的前n项和Sn.
}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,椭圆
两点,椭圆![]() 的右顶点为
的右顶点为![]() ,且满足
,且满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() ,且定点
,且定点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形.
为正三角形.
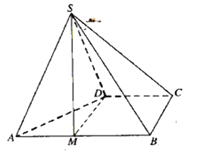
(1)点![]() 为棱
为棱![]() 上一点,若
上一点,若![]() 平面
平面![]() ,
,![]() ,求实数
,求实数![]() 的值;
的值;
(2)求点B到平面SAD的距离.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由![]() 平面
平面![]() ,可证
,可证![]() ,进而证得四边形
,进而证得四边形![]() 为平行四边形,根据
为平行四边形,根据![]() ,可得
,可得![]() ;
;
(2)利用等体积法![]() 可求点
可求点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:((1)因为![]() 平面SDM,
平面SDM,
![]()
![]() 平面ABCD,
平面ABCD,
平面SDM ![]() 平面ABCD=DM,
平面ABCD=DM,
所以![]() ,
,
因为![]() ,所以四边形BCDM为平行四边形,又
,所以四边形BCDM为平行四边形,又![]() ,所以M为AB的中点.
,所以M为AB的中点.
因为![]() ,
,
![]() .
.

(2)因为![]()
![]() ,
, ![]()
![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
在平面![]() 内过点
内过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,
,
在![]() 和
和![]() 中,
中,
因为![]() ,所以
,所以![]() ,
,
又由题知![]() ,
,
所以![]() ,
,
由已知求得![]() ,所以
,所以![]() ,
,
连接BD,则![]() ,
,
又求得![]() 的面积为
的面积为![]() ,
,
所以由![]() 点B 到平面
点B 到平面![]() 的距离为
的距离为![]() .
.
【题型】解答题
【结束】
19
【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(1)请分别求出甲、乙两种薪酬方案中日薪![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数与天数满足以下表格:
日均派送单数 | 52 | 54 | 56 | 58 | 60 |
频数(天) | 20 | 30 | 20 | 20 | 10 |
回答下列问题:
①根据以上数据,设每名派送员的日薪为![]() (单位:元),试分别求出这100天中甲、乙两种方案的日薪
(单位:元),试分别求出这100天中甲、乙两种方案的日薪![]() 平均数及方差;
平均数及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在
在![]() 处的切线经过点
处的切线经过点![]() .
.
(1)证明: ![]() ;
;
(2)若当![]() 时,
时, 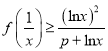 ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)先根据导数几何意义得切线斜率为![]() ,再根据切线过点
,再根据切线过点![]() ,解得
,解得![]() 导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为
导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为![]() ,分离得
,分离得![]() ,再利用导数求函数
,再利用导数求函数![]() 单调性,利用罗伯特法则求最大值,即得
单调性,利用罗伯特法则求最大值,即得![]() 的取值范围.
的取值范围.
试题解析:(1)曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,即
,即![]()
由题意得![]() ,解得
,解得![]()
所以![]()
从而![]()
因为当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
所以![]() 在区间
在区间![]() 上是减函数,区间
上是减函数,区间![]() 上是增函数,
上是增函数,
从而![]() .
.
(2)由题意知,当![]() 时,
时, ![]() ,所以
,所以![]()
从而当![]() 时,
时, ![]() ,
,
由题意知 ,即
,即![]() ,其中
,其中![]()
设![]() ,其中
,其中![]()
设![]() ,即
,即![]() ,其中
,其中![]()
则![]() ,其中
,其中![]()
(1)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是增函数
是增函数
从而当![]() 时,
时, ![]() ,
,
所以![]() 是增函数,从而
是增函数,从而![]() .
.
故当![]() 时符合题意.
时符合题意.
(2)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上是减函数
上是减函数
从而当![]() 时,
时, ![]()
所以![]() 在
在![]() 上是减函数,从而
上是减函数,从而![]()
故当![]() 时不符合题意.
时不符合题意.
(3)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是减函数
是减函数
从而当![]() 时,
时, ![]()
所以![]() 是减函数,从而
是减函数,从而![]()
故当![]() 时不符合题意
时不符合题意
综上![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
22
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: ![]() .以
.以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴,与直角坐标系
轴的非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.
取相同的长度单位,建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的异于极点的交点为
的异于极点的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com