
【题目】如图所示,在棱长为1的正方体![]() 中,点
中,点![]() 分别是棱
分别是棱![]() 的中点,
的中点,![]() 是侧面
是侧面![]() 内一点,若
内一点,若![]() 平面
平面![]() ,则线段
,则线段![]() 长度的取值范围是( )
长度的取值范围是( )

A. B.
B. C.
C. D.
D.![]()
【答案】B
【解析】
分别取棱BB1、B1C1的中点M、N,连接MN,易证平面A1MN∥平面AEF,由题意知点P必在线段MN上,由此可判断P在M或N处时A1P最长,位于线段MN中点处时最短,通过解直角三角形即可.
如图所示:分别取棱BB1、B1C1的中点M、N,连接MN,连接BC1,
∵M、N、E、F为所在棱的中点,∴MN∥BC1,EF∥BC1,
∴MN∥EF,又MN平面AEF,EF平面AEF,∴MN∥平面AEF;
∵AA1∥NE,AA1=NE,∴四边形AENA1为平行四边形,
∴A1N∥AE,又A1N平面AEF,AE平面AEF,∴A1N∥平面AEF,
又A1N∩MN=N,∴平面A1MN∥平面AEF,∵P是侧面BCC1B1内一点,且A1P∥平面AEF,
则P必在线段MN上,在Rt△A1B1M中,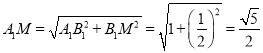 ,
,
同理,在Rt△A1B1N中,求得A1N=![]() ,∴△A1MN为等腰三角形,
,∴△A1MN为等腰三角形,
当P在MN中点O时A1P⊥MN,此时A1P最短,P位于M、N处时A1P最长,
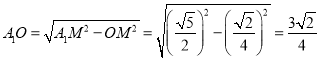 ,A1M=A1N=
,A1M=A1N=![]() ,
,
所以线段A1P长度的取值范围是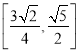 .
.
故选B.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某医疗器械公司在全国共有![]() 个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这
个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这![]() 个销售点的年销量绘制出如下的频率分布直方图.
个销售点的年销量绘制出如下的频率分布直方图.
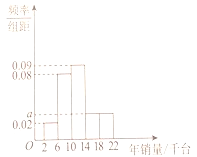
(1)完成年销售任务的销售点有多少个?
(2)若用分层抽样的方法从这![]() 个销售点中抽取容量为
个销售点中抽取容量为![]() 的样本,求该五组
的样本,求该五组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(单位:千台)中每组分别应抽取的销售点数量.
,(单位:千台)中每组分别应抽取的销售点数量.
(3)在(2)的条件下,从该样本中完成年销售任务的销售点中随机选取![]() 个,求这两个销售点不在同一组的概率.
个,求这两个销售点不在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-P2-x,则下列结论正确的是( )
A. ![]() ,
,![]() 为奇函数且为R上的减函数
为奇函数且为R上的减函数
B. ![]() ,
,![]() 为偶函数且为R上的减函数
为偶函数且为R上的减函数
C. ![]() ,
,![]() 为奇函数且为R上的增函数
为奇函数且为R上的增函数
D. ![]() ,
,![]() 为偶函数且为R上的增函数
为偶函数且为R上的增函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲袋内摸出1个红球的概率是![]() ,从乙袋内摸出1个红球的概率是
,从乙袋内摸出1个红球的概率是![]() ,从两袋内各摸出1个球,则
,从两袋内各摸出1个球,则![]() 等于( )
等于( )
A. 2个球不都是红球的概率B. 2个球都是红球的概率
C. 至少有1个红球的概率D. 2个球中恰好有1个红球的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com