
【题目】已知![]() .
.
(1)当![]() 时,求证:
时,求证:![]() 在
在![]() 上单调递减;
上单调递减;
(2)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】为实现2020年全面建设小康社会,某地进行产业的升级改造.经市场调研和科学研判,准备大规模生产某高科技产品的一个核心部件,目前只有甲、乙两种设备可以独立生产该部件.如图是从甲设备生产的部件中随机抽取400件,对其核心部件的尺寸x,进行统计整理的频率分布直方图.
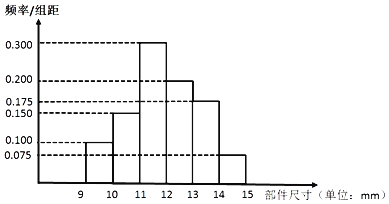
根据行业质量标准规定,该核心部件尺寸x满足:|x﹣12|≤1为一级品,1<|x﹣12|≤2为二级品,|x﹣12|>2为三级品.
(Ⅰ)现根据频率分布直方图中的分组,用分层抽样的方法先从这400件样本中抽取40件产品,再从所抽取的40件产品中,抽取2件尺寸x∈[12,15]的产品,记ξ为这2件产品中尺寸x∈[14,15]的产品个数,求ξ的分布列和数学期望;
(Ⅱ)将甲设备生产的产品成箱包装出售时,需要进行检验.已知每箱有100件产品,每件产品的检验费用为50元.检验规定:若检验出三级品需更换为一级或二级品;若不检验,让三级品进入买家,厂家需向买家每件支付200元补偿.现从一箱产品中随机抽检了10件,结果发现有1件三级品.若将甲设备的样本频率作为总体的慨率,以厂家支付费用作为决策依据,问是否对该箱中剩余产品进行一一检验?请说明理由;
(Ⅲ)为加大升级力度,厂家需增购设备.已知这种产品的利润如下:一级品的利润为500元/件;二级品的利润为400元/件;三级品的利润为200元/件.乙种设备产品中一、二、三级品的概率分别是![]() ,
,![]() ,
,![]() .若将甲设备的样本频率作为总体的概率,以厂家的利润作为决策依据.应选购哪种设备?请说明理由.
.若将甲设备的样本频率作为总体的概率,以厂家的利润作为决策依据.应选购哪种设备?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
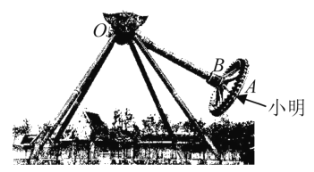
【题目】如图,大摆锤是一种大型的游乐设备,常见于各大游乐园.游客坐在圆形的座舱中,面向外.通常,大摆锤以压肩作为安全束缚,配以安全带作为二次保险.座舱旋转的同时,悬挂座舱的主轴在电机的驱动下做单摆运动.大摆锤的运行可以使置身其上的游客惊心动魄.今年元旦,小明去某游乐园玩“大摆锤”,他坐在点![]() 处,“大摆锤”启动后,主轴
处,“大摆锤”启动后,主轴![]() 在平面
在平面![]() 内绕点
内绕点![]() 左右摆动,平面
左右摆动,平面![]() 与水平地面垂直,
与水平地面垂直,![]() 摆动的过程中,点
摆动的过程中,点![]() 在平面
在平面![]() 内绕点
内绕点![]() 作圆周运动,并且始终保持
作圆周运动,并且始终保持![]() ,
,![]() ,已知
,已知![]() ,在“大摆锤”启动后,下列
,在“大摆锤”启动后,下列![]() 个结论中正确的是______(请填上所有正确结论的序号).
个结论中正确的是______(请填上所有正确结论的序号).
①点![]() 在某个定球面上运动;
在某个定球面上运动;
②线段![]() 在水平地面上的正投影的长度为定值;
在水平地面上的正投影的长度为定值;
③直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]() ;
;
④直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求曲线C的极坐标方程和直线l的直角坐标方程;
(2)若射线![]() 与曲线C交于点A(不同于极点O),与直线l交于点B,求
与曲线C交于点A(不同于极点O),与直线l交于点B,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位一辆交通车载有8个职工从单位出发送他们下班回家,途中共有甲、乙、丙3个停车点.如果某停车点无人下车,那么该车在这个点就不停车.假设每个职工在每个停车点下车的可能性都是相等的,求下列事件的概率:
(1)该车在某停车点停车;
(2)停车的次数不少于2次;
(3)恰好停车2次.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为![]() ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为![]() ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为![]() .
.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com