
(1)如果![]() =e1+e2,
=e1+e2,![]() =2e1+8e2,
=2e1+8e2,![]() =3(e1,-e2),求证:A、B、D三点共线;
=3(e1,-e2),求证:A、B、D三点共线;
(2)试确定实数k,使ke1+e2和e1+ke2共线.
思路分析:本题主要考查向量基本定理和向量共线的条件.(1)可以将e1,e2看作一组基底表示我们需要的向量,如![]() ,
,![]() =
=![]() +
+![]() =2e1+8e2+3e1-3e2=5e1+5e2然后利用向量共线条件进行证明.(2)由于向量ke1+e2,e1+ke2都是用基底e1,e2表示出来的两个向量,既然两向量共线,就可以用共线条件得到(ke1+e2)=λ(e1+ke2),解出k值即可.
=2e1+8e2+3e1-3e2=5e1+5e2然后利用向量共线条件进行证明.(2)由于向量ke1+e2,e1+ke2都是用基底e1,e2表示出来的两个向量,既然两向量共线,就可以用共线条件得到(ke1+e2)=λ(e1+ke2),解出k值即可.
(1)证明:∵![]() =e1+e2,
=e1+e2,
![]() +
+![]()
=2e1+8e2+3e1-3e2
=5(e1+e2)=5![]() ,
,
∴![]() 、BD共线.又有公共点B,∴A、B、D三点共线.
、BD共线.又有公共点B,∴A、B、D三点共线.
(2)解:∵ke1+e2与e1+ke2共线,
∴存在λ使ke1+e2=λ(e1+ke2),
则(k-λ)e1=(λk-1)e2.由于e1与e2不共线,
∴只能有![]() 则k=±1.
则k=±1.
温馨提示
题目中已给出一组基底e1,e2,则该平面中任一向量都可以与之建立联系,以该基底为纽带,可以沟通不同向量之间的联系.本题要证三点共线,由这三点中任意两点确定两个向量.然后用基底e1,e2表示,并依据向量共线的条件来证明这两个向量共线.又这两个向量有公共点,于是证三点共线.


科目:高中数学 来源: 题型:
| AB |
| BC |
| CD |
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修4 2.5向量的应用练习卷(解析版) 题型:解答题
设两非零向量e1和e2不共线.
(1)如果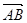 =
=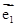 +
+ 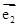 ,
, =2
=2 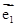 +8
+8 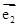 ,
,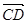 =3(
=3(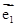 -
-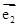 ),求证:A、B、D三点共线;
),求证:A、B、D三点共线;
(2)试确定实数k,使k 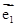 +
+ 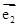 和
和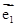 +k
+k 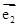 共线;
共线;
(3)若| 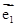 |=2,|
|=2,| 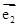 |=3,
|=3, 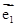 与
与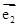 的夹角为60°,试确定k的值,使k
的夹角为60°,试确定k的值,使k 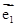 +
+ 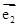 与
与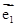 +k
+k 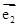 垂直.
垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)如果![]() =e1+e2,
=e1+e2,![]() =2e1+8e2,
=2e1+8e2,![]() =3(e1-e2),求证:A、B、D三点共线;
=3(e1-e2),求证:A、B、D三点共线;
(2)试确定实数k,使ke1+e2和e1+ke2共线.
查看答案和解析>>
科目:高中数学 来源:《2.4-2.5 平面向量的数量积及平面向量的应用举例》2011年同步练习(解析版) 题型:解答题
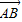 =e1+e2,
=e1+e2, =2e1+8e2,
=2e1+8e2,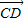 =3(e1-e2),求证:A、B、D三点共线;
=3(e1-e2),求证:A、B、D三点共线;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com