
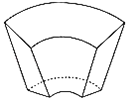
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗЪЧЮвЙњЙХДњФкШнМЋЮЊЗсИЛЕФЪ§бЇУћжјЃЌЪщжагаШчЯТЮЪЬтЃКЁАНёгаЧњГиЃЌЩЯжажмЖўеЩЃЌЭтжмЫФеЩЃЌЙувЛеЩЃЌЯТжажмвЛеЩЫФГпЃЌЭтжмЖўеЩЫФГпЃЌЙуЮхГпЃЌЩювЛеЩЃЌЮЪЛ§МИКЮЃПЁБЦфвтЫМЮЊЃКЁАНёгаЩЯЯТЕзУцНдЮЊЩШаЮЕФЫЎГиЃЌЩЯЕзжажм2еЩЃЌЭтжм4еЩЃЌПэ1еЩЃЛЯТЕзжажм1еЩ4ГпЃЌЭтжмГЄ2еЩ4ГпЃЌПэ5ГпЃЛЩю1еЩЃЎЮЪЫќЕФШнЛ§ЪЧЖрЩйЃПЁБдђИУЧњГиЕФШнЛ§ЮЊЃЈ ЃЉСЂЗНГпЃЈ1еЩЃН10ГпЃЌЧњГиЃКЩЯЯТЕзУцНдЮЊЩШаЮЕФЭСГиЃЌЦфШнЛ§ЙЋЪНЮЊ![]() [ЃЈ2ЁСЩЯПэ+ЯТПэЃЉ
[ЃЈ2ЁСЩЯПэ+ЯТПэЃЉ![]() ЃЈ2ЁСЯТПэ+ЩЯПэЃЉ
ЃЈ2ЁСЯТПэ+ЩЯПэЃЉ![]() ]ЁСЩюЃЉ
]ЁСЩюЃЉ
A.![]() B.1890C.
B.1890C.![]() D.
D.![]()
 НнОЖбЕСЗМьВтОэЯЕСаД№АИ
НнОЖбЕСЗМьВтОэЯЕСаД№АИ аЁЗђзгШЋФмМьВтЯЕСаД№АИ
аЁЗђзгШЋФмМьВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛжжЫЎЙћЕФОбщБэУїЃЌИУЫЎЙћУПШеЕФЯњЪлСП![]() ЃЈЕЅЮЛЃКЧЇПЫЃЉгыЯњЪлМлИё
ЃЈЕЅЮЛЃКЧЇПЫЃЉгыЯњЪлМлИё![]() ЃЈЕЅЮЛЃКдЊ/ЧЇПЫЃЉТњзуЙиЯЕЪН
ЃЈЕЅЮЛЃКдЊ/ЧЇПЫЃЉТњзуЙиЯЕЪН![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЮЊГЃЪ§.вбжЊЯњЪлМлИёЮЊ6дЊ/ЧЇПЫЪБЃЌУПШеПЩЪлГіИУЫЎЙћ52ЧЇПЫ.
ЮЊГЃЪ§.вбжЊЯњЪлМлИёЮЊ6дЊ/ЧЇПЫЪБЃЌУПШеПЩЪлГіИУЫЎЙћ52ЧЇПЫ.
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШєИУЫЎЙћЕФГЩБОЮЊ5дЊ/ЧЇПЫЃЌЪдШЗЖЈЯњЪлМлИё![]() ЕФжЕЃЌЪЙЩЬГЁУПШеЯњЪлИУЫЎЙћЫљЛёЕУЕФРћШѓзюДѓЃЌВЂЧѓГізюДѓРћШѓ.
ЕФжЕЃЌЪЙЩЬГЁУПШеЯњЪлИУЫЎЙћЫљЛёЕУЕФРћШѓзюДѓЃЌВЂЧѓГізюДѓРћШѓ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЮЊе§ЗНаЮЃЌ
ЮЊе§ЗНаЮЃЌ![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
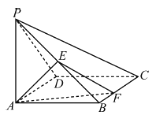
ЃЈ1ЃЉШє![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯЕФЖЏЕуЃЌжЄУїЃКЦНУц
ЩЯЕФЖЏЕуЃЌжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЩЯЕФЖЏЕуЃЈВЛКЌ
ЩЯЕФЖЏЕуЃЈВЛКЌ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ![]() ЃЌШ§РтзЖ
ЃЌШ§РтзЖ![]() ЕФЬхЛ§ЪЧЗёДцдкзюДѓжЕЃПШчЙћДцдкЃЌЧѓГізюДѓжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФЬхЛ§ЪЧЗёДцдкзюДѓжЕЃПШчЙћДцдкЃЌЧѓГізюДѓжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЧњЯп![]() ЩЯШЮвтвЛЕу
ЩЯШЮвтвЛЕу![]() Тњзу
Тњзу![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЌЧвгыЧњЯп
ЃЌЧвгыЧњЯп![]() НЛгкВЛЭЌСНЕу
НЛгкВЛЭЌСНЕу![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() гы
гы![]() ЕФаБТЪЗжБ№ЮЊ
ЕФаБТЪЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌХаЖЯжБЯп
ЃЌХаЖЯжБЯп![]() ЪЧЗёЙ§ЖЈЕуЃПШєЙ§ЖЈЕуЃЌЧѓИУЖЈЕуЕФзјБъ.
ЪЧЗёЙ§ЖЈЕуЃПШєЙ§ЖЈЕуЃЌЧѓИУЖЈЕуЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯпlЕФВЮЪ§ЗНГЬЮЊ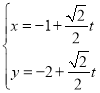 ЃЈtЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуOЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯпCЕФМЋзјБъЗНГЬЮЊІбsin2ІШЃН4acosІШЃЌжБЯпlгыЧњЯпCНЛгкВЛЭЌЕФСНЕуMЃЌNЃЎ
ЃЈtЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуOЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯпCЕФМЋзјБъЗНГЬЮЊІбsin2ІШЃН4acosІШЃЌжБЯпlгыЧњЯпCНЛгкВЛЭЌЕФСНЕуMЃЌNЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉвбжЊaЃО0ЃЌЩшЕуPЃЈЉ1ЃЌЉ2ЃЉЃЌШє|PM|ЃЌ|MN|ЃЌ|PN|ГЩЕШБШЪ§СаЃЌЧѓaЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌИУМИКЮЬхЪЧгЩвЛИіжБШ§РтжљABEЉDCFКЭвЛИіЫФРтзЖPЉABCDзщКЯЖјГЩЃЌЦфжаEFЃНEAЃНEBЃН2ЃЌAEЁЭEBЃЌPAЃНPD![]() ЃЌЦНУцPADЁЮЦНУцEBCFЃЎ
ЃЌЦНУцPADЁЮЦНУцEBCFЃЎ
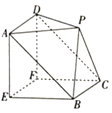
ЃЈ1ЃЉжЄУїЃКЦНУцPBCЁЮЦНУцAEFDЃЛ
ЃЈ2ЃЉЧѓжБЯпAPгыЦНУцPCDЫљГЩНЧЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП1772ФъЕТЙњЕФЬьЮФбЇМвВЈЕУЗЂЯжСЫЧѓЬЋбєЕФаааЧОрРыЕФЗЈдђЃЌМЧЕиЧђОрРыЬЋбєЕФЦНОљОрРыЮЊ10ЃЌПЩвдЫуЕУЕБЪБвбжЊЕФСљДѓаааЧОрРыЬЋбєЕФЦНОљОрРыШчЯТБэЃК
аЧУћ | ЫЎаЧ | Н№аЧ | ЕиЧђ | Л№аЧ | ФОаЧ | ЭСаЧ |
гыЬЋбєЕФОрРы | 4 | 7 | 10 | 16 | 52 | 100 |
Г§ЫЎаЧЭтЃЌЦфгрИїаЧгыЬЋбєЕФОрРыЖМТњзуВЈЕУЖЈдђЃЈФГвЛЪ§СаЙцТЩЃЉЃЌЕБЪБЕТЙњЪ§бЇМвИпЫЙИљОнДЫЖЈдђЭЦЫуЃЌЛ№аЧКЭФОаЧжЎМфОрРыЬЋбє28ЛЙгавЛПХДѓаааЧЃЌ1801ФъЃЌвтДѓРћЬьЮФбЇМвЦЄбЧЦыОЙ§ЙлВтЃЌЙћШЛевЕНСЫЛ№аЧКЭФОаЧжЎМфОрРыЬЋбє28ЕФЙШЩёаЧвдМАЫќЫљдкЕФаЁаааЧДјЃЌЧыФуИљОнетИіЖЈдђЃЌЙРЫуДгЫЎаЧПЊЪМгЩНќЕНдЖЫуЃЌЕк10ИіаааЧгыЬЋбєЕФЦНОљОрРыДѓдМЪЧЃЈ ЃЉ
A.388B.772C.1540D.3076
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЮЊзјБъдЕуЃЌ
ЮЊзјБъдЕуЃЌ![]() ЪЧХзЮяЯп
ЪЧХзЮяЯп![]() ЃК
ЃК![]() ЕФНЙЕуЃЌ
ЕФНЙЕуЃЌ![]() ЪЧХзЮяЯп
ЪЧХзЮяЯп![]() ЩЯЮЛгкЕквЛЯѓЯоФкЕФШЮвтвЛЕуЃЌЙ§
ЩЯЮЛгкЕквЛЯѓЯоФкЕФШЮвтвЛЕуЃЌЙ§![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕуЕФдВЕФдВаФЮЊ
Ш§ЕуЕФдВЕФдВаФЮЊ![]() .
.
ЃЈ1ЃЉЪЧЗёДцдкЙ§Еу![]() ЃЌаБТЪЮЊ
ЃЌаБТЪЮЊ![]() ЕФжБЯп
ЕФжБЯп![]() ЃЌЪЙЕУХзЮяЯп
ЃЌЪЙЕУХзЮяЯп![]() ЩЯДцдкСНЕуЙигкжБЯп
ЩЯДцдкСНЕуЙигкжБЯп![]() ЖдГЦЃПШєДцдкЃЌЧѓГі
ЖдГЦЃПШєДцдкЃЌЧѓГі![]() ЕФЗЖЮЇЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЕФЗЖЮЇЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЪЧЗёДцдкЕу![]() ЃЌЪЙЕУжБЯп
ЃЌЪЙЕУжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЯрЧагкЕу
ЯрЧагкЕу![]() ЃПШєДцдкЃЌЧѓГіЕу
ЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЈЕу![]() ЃЌдВ
ЃЌдВ![]() ЃЌЙ§RЕуЕФжБЯп
ЃЌЙ§RЕуЕФжБЯп![]() НЛдВгкMЃЌNСНЕуЙ§RЕузїжБЯп
НЛдВгкMЃЌNСНЕуЙ§RЕузїжБЯп![]() НЛSMгкQЕу.
НЛSMгкQЕу.
ЃЈ1ЃЉЧѓQЕуЕФЙьМЃЗНГЬЃЛ
ЃЈ2ЃЉШєAЃЌBЮЊQЕФЙьМЃгыxжсЕФзѓгвНЛЕуЃЌ![]() ЮЊИУЙьМЃЩЯШЮвЛЖЏЕуЃЌЩшжБЯпAPЃЌBPЗжБ№НЛжБЯпlЃК
ЮЊИУЙьМЃЩЯШЮвЛЖЏЕуЃЌЩшжБЯпAPЃЌBPЗжБ№НЛжБЯпlЃК![]() гкЕуMЃЌNЃЌХаЖЯвдMNЮЊжБОЖЕФдВЪЧЗёЙ§ЖЈЕуЁЃШчдВЙ§ЖЈЕуЃЌдђЧѓГіИУЖЈЕуЃЛШчВЛЪЧЃЌЫЕУїРэгЩ.
гкЕуMЃЌNЃЌХаЖЯвдMNЮЊжБОЖЕФдВЪЧЗёЙ§ЖЈЕуЁЃШчдВЙ§ЖЈЕуЃЌдђЧѓГіИУЖЈЕуЃЛШчВЛЪЧЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com