解:设事件A
I(i=1,2,3,4)表示“该应聘人员能通过第i轮考查”,由已知,得P(A
1)=

,P(A
2)=

,P(A
3)=

,P(A
4)=

(1)设事件C表示“该应聘人员至多进入面试”,则P(C)=P(

+

+
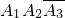
)=P(

)+P(

)+P(
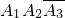
)=

+

+

=

,
(2)依题意知随机变量X的可能取值分别为1,2,3,4且P(X=1)=P(

)=

,P(X=2)=P(

)=

P(X=3)=P(
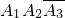
)=

P(X=4)=P(A
1A
2A
3)=
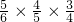
=

所以随机变量X的分布列为
随机变量的期望值EX=
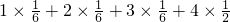
=3
分析:(1)“该应聘人员至多进入面试”这个事件包括了初审、笔试、面试三个环节落选,此三者是互斥的,后一个环节落选地是前面通过的基础上发生的,故需要用到概率的加法公式与互相独立事件的概率乘法公式,先分类再分步.
(2)随机变量X的可能取值分别为1,2,3,4,建立变量X的可能取值与应聘人员进入某一个环节的对应,即可求得相应的概率,列出分布列,计算出期望值.
点评:本题考点是离散型随机变量与其分布列,考查了相互独立事件的概率的乘法公式以及分布列的求法,期望的求法,本题属于概率中综合性较强的题目,属于概率的应用题,这几年高考中对概率的应用的考查开始增多,对此类题要做彻底的研究.

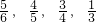 ,且各轮能否通过互不影响.
,且各轮能否通过互不影响. ,P(A2)=
,P(A2)= ,P(A3)=
,P(A3)= ,P(A4)=
,P(A4)=
 +
+ +
+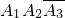 )=P(
)=P( )+P(
)+P( )+P(
)+P(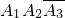 )=
)= +
+ +
+ =
= ,
, )=
)= ,P(X=2)=P(
,P(X=2)=P( )=
)=
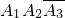 )=
)=
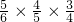 =
=




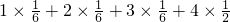 =3
=3

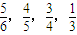 ,且各轮能否通过互不影响.
,且各轮能否通过互不影响.