
如图 ,在四棱锥
,在四棱锥 中,
中,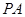
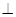 平面
平面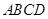 ,底面
,底面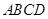 是菱形,点O是对角线
是菱形,点O是对角线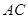 与
与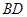 的交点,
的交点,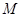 是
是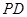 的中点,
的中点,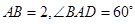 .
.

(1) 求证: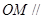 平面
平面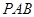 ;
;
(2) 平面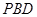
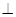 平面
平面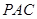 ;
;
(3) 当四棱锥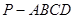 的体积等于
的体积等于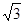 时,求
时,求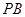 的长.
的长.
(1)答案见解析
(2)答案见解析
(3)PB=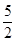
【解析】试题分析:(I)利用线面平行的判定定理只要证OM//PB即可.
(II)根据面面垂直的判定定理只要证: 即可,因为
即可,因为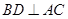 ,只要证:
,只要证: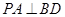 .
.
(III)因为底面积易求,利用棱锥的体积公式,可求出高PA,再在直角三角形PAB中,利用勾股定理求出PB的值.
解:(1) 在
在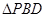 中,
中,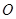 、
、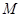 分别是
分别是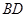 、
、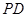 的中点,
的中点,
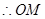 是
是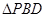 的中位线,
的中位线,
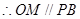 ,
…………1分
,
…………1分
 平面
平面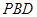 ,
,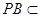 平面
平面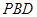 ,……3分
,……3分
 平面
平面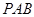 .
…………4分
.
…………4分
(2) 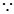 底面
底面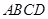 是菱形,
是菱形,
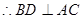 ,
…………5分
,
…………5分
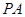
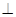 平面
平面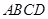 ,
,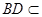 平面
平面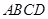
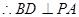 .
…………6分
.
…………6分
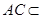 平面
平面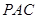 ,
,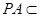 平面
平面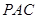 ,
,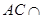
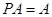 ,…………7分
,…………7分
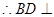 平面
平面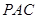 ,
…………8分
,
…………8分
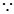
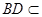 平面
平面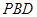 ,
…………9分
,
…………9分
 平面
平面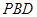
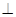 平面
平面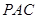 .
…………10分
.
…………10分
(3)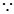 底面
底面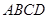 是菱形,
是菱形,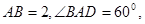
 菱形
菱形 的面积为
的面积为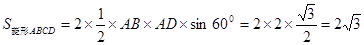 ,…………11分
,…………11分
 四棱锥
四棱锥 的高为
的高为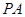 ,
,
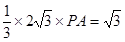 ,得
,得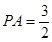 …………12分
…………12分
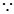
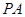
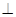 平面
平面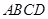 ,
,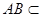 平面
平面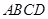 ,
,
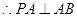 .
…………13分
.
…………13分
在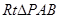 中,
中,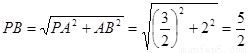 .
…………14分
.
…………14分
考点:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.
点评:掌握线线,线面,面面平行与垂直的判定与性质是解决此类问题的关键.同时还要记住柱、锥、台体的体积及表面积公式.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
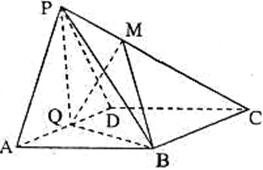
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.查看答案和解析>>
科目:高中数学 来源: 题型:
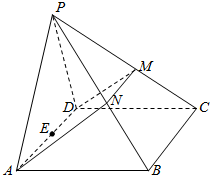 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥
如图,在四棱锥![]() 中,侧面
中,侧面![]()
是正三角形,且与底面![]() 垂直,底面
垂直,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 是
是![]() 中点,过
中点,过![]() 、
、![]() 、
、![]() 三点的平面交
三点的平面交![]() 于
于![]() .
.
(1)求证:![]() ; (2)求证:
; (2)求证:![]() 是
是![]() 中点;(3)求证:平面
中点;(3)求证:平面![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 的中点。
的中点。![]()
(1)点![]() 在线段
在线段![]() 上,
上,![]() ,
,
 试确定
试确定![]() 的值,使
的值,使![]() 平面
平面![]() ;
;
(2)在(1)的条件下,若平面![]() 平
平
面ABCD,求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 的中点。
的中点。

![]()
(1)点![]() 在线段
在线段![]() 上,
上,![]() ,
,
试确定![]() 的值,使
的值,使![]() 平面
平面![]() ;
;
(2)在(1)的条件下,若平面![]() 平
平
面ABCD,求二面角![]() 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com