
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)根据二倍角公式![]() ,三角形内角和
,三角形内角和![]() ,所以
,所以![]() ,整理为关于
,整理为关于![]() 的二次方程,解得角
的二次方程,解得角![]() 的大小;(2)根据三角形的面积公式和上一问角
的大小;(2)根据三角形的面积公式和上一问角![]() ,代入后解得边
,代入后解得边![]() ,这样就知道
,这样就知道![]() ,然后根据余弦定理再求
,然后根据余弦定理再求![]() ,最后根据证得定理分别求得
,最后根据证得定理分别求得![]() 和
和![]() .
.
试题解析:(1)由cos 2A-3cos(B+C)=1,
得2cos2A+3cos A-2=0,
即(2cos A-1)(cos A+2)=0,
解得cos A=![]() 或cos A=-2(舍去).
或cos A=-2(舍去).
因为0<A<π,所以A=![]() .
.
(2)由S=![]() bcsin A=
bcsin A=![]() bc×
bc×![]() =
=![]() bc=5
bc=5![]() ,得bc=20,又b=5,知c=4.
,得bc=20,又b=5,知c=4.
由余弦定理得a2=b2+c2-2bccos A=25+16-20=21,故a=![]() .
.
从而由正弦定理得sin B sin C=![]() sin A×
sin A×![]() sin A=
sin A=![]() sin2A=
sin2A=![]() ×
×![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】若函数exf(x)(e=2.71828…,是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数:
①f(x)=![]() (x>1) ②f(x)=x2 ③f(x)=cosx ④f(x)=2-x
(x>1) ②f(x)=x2 ③f(x)=cosx ④f(x)=2-x
中具有M性质的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+![]() .
.
(I)当a=![]() 时,求函数f(x)在x=0处的切线方程;
时,求函数f(x)在x=0处的切线方程;
(II)函数f(x)是否存在零点?若存在,求出零点的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某植物园准备建一个五边形区域的盆栽馆,三角形ABE为盆裁展示区,沿AB、AE修建观赏长廊,四边形BCDE是盆栽养护区,若BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=![]() 米。
米。
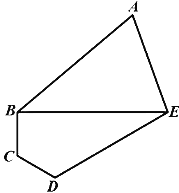
(1)求两区域边界BE的长度;
(2)若区域ABE为锐角三角形,求观赏长廊总长度AB+AE的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂为检验车间一生产线是否工作正常,现从生产线中随机抽取一批零件样本,测量尺寸(单位: mm )绘成频率分布直方图如图所示:
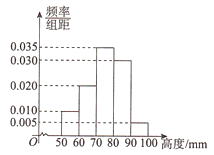
(Ⅰ)求该批零件样本尺寸的平均数 x 和样本方差 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)若该批零件尺寸![]() 服从正态分布
服从正态分布 ![]() ,其中
,其中 ![]() 近似为样本平均数
近似为样本平均数 ![]() 近似为样本方差
近似为样本方差 ![]() ,利用该正态分布求
,利用该正态分布求 ![]() ;
;
(Ⅲ)若从生产线中任取一零件,测量尺寸为30mm,根据 ![]() 原则判断该生产线是否正常?
原则判断该生产线是否正常?
附: ![]() ;若
;若![]() ,则
,则 ![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
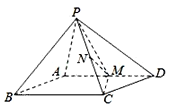
【题目】如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD.M是AD的中点,N是PC的中点.
(1)求证:MN∥平面PAB;
(2)若平面PMC⊥平面PAD,求证:CM⊥AD;
(3)若平面ABCD是矩形,PA=AB,求证:平面PMC⊥平面PBC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com