
【题目】已知△ABC的三边所在直线的方程分别是lAB:4x-3y+10=0,lBC:y=2,lCA:3x-4y=5.
(1)求∠BAC的平分线所在直线的方程;
(2)求AB边上的高所在直线的方程.
【答案】(1)7x-7y+5=0;(2)3x+4y-21=0.
【解析】
(1)设P(x,y)是∠BAC的平分线上任意一点,根据点P到AC,AB的距离相等求出∠BAC的平分线所在直线的方程.(2) 设过点C的直线系方程为3x-4y-5+λ(y-2)=0,根据此直线与直线lAB:4x-3y+10=0垂直得到λ的值,即得AB边上的高所在直线的方程.
(1)设P(x,y)是∠BAC的平分线上任意一点,
则点P到AC,AB的距离相等,即![]() =
=![]() ,
,
∴4x-3y+10=±(3x-4y-5).
又∵∠BAC的平分线所在直线的斜率在![]() 和
和![]() 之间,
之间,
∴7x-7y+5=0为∠BAC的平分线所在直线的方程.
(2)设过点C的直线系方程为3x-4y-5+λ(y-2)=0,
即3x-(4-λ)y-5-2λ=0.
若此直线与直线lAB:4x-3y+10=0垂直,
则3×4+3(4-λ)=0,解得λ=8.
故AB边上的高所在直线的方程为3x+4y-21=0.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为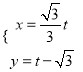 ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)求直线![]() 与曲线
与曲线![]() 的交点的直角坐标.
的交点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中曲线C1:ρ=1,  (t为参数).
(t为参数).
(Ⅰ)求曲线C1上的点到曲线C2距离的最小值;
(Ⅱ)若把C1上各点的横坐标都扩大为原来的2倍,纵坐标扩大为原来的 ![]() 倍,得到曲线
倍,得到曲线 ![]() .设P(﹣1,1),曲线C2与
.设P(﹣1,1),曲线C2与 ![]() 交于A,B两点,求|PA|+|PB|.
交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1和l2的距离是![]() .
.
(1)求a的值.
(2)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l1的距离是P点到l2的距离的![]() ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是![]() ?若能,求出P点坐标;若不能,请说明理由.
?若能,求出P点坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 从
从![]() ,
, ![]() ,
, ![]() ,
, ![]() 四个数中任取的一个数,
四个数中任取的一个数, ![]() 是从
是从![]() ,
, ![]() ,
, ![]() 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司购买了一块长AM=30米,宽AN=20米的矩形地块,计划把图中矩形ABCD建设为仓库,其余地方为道路和停车场,要求顶点C在地块对角线MN上,B、D分别在边AM、AN上,假设AB的长度为x米

(1)求矩形ABCD的面积S关于x的函数解析式;
(2)要使仓库占地ABCD的面积不少于144平方米,则AB的长度应在什么范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com