Question

【题目】已知椭圆的离心率是，点在椭圆上，A，B分别为椭圆的右顶点与上顶点，过点A，B引椭圆C的两条弦AE、BF交椭圆于点E，F．

求椭圆C的方程；

若直线AE，BF的斜率互为相反数，

求出直线EF的斜率；

若O为直角坐标原点，求面积的最大值．

Answer 1

【答案】（1）；（2）直线EF的斜率,面积的最大值.

【解析】

根据椭圆的离心率公式，将点代入椭圆方程，即可求得a和b的值，求得椭圆方程；

设直线AE及BF的方程，代入椭圆方程，求得E和F点坐标，根据直线的斜率公式，即可直线EF的斜率；

设直线EF的方程，代入椭圆方程，利用韦达定理及弦长公式求得，根据三角形的面积公式及二次函数的性质，即可求得答案．

解：由椭圆的离心率，

则，将点代入椭圆方程：，

解得，，

椭圆的标准方程：；

设，，直线AE的方程：，

联立，整理得：，

解得：，或，

，

设直线BF的方程为：，联立，

整理得：，解得：或，

，则直线EF的斜率，

直线EF的斜率；

设直线EF的方程：，，

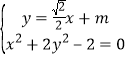整理得：，

，则，

则，，

，

O到直线EF的距离，则，

设，，，

时，取最大值，最大值为，

面积的最大值．