
【题目】已知函数f(x)=log2x,x∈(4,8),则函数y=f(x2)+ ![]() 的值域为( )
的值域为( )
A.[8,10)
B.( ![]() ,10)
,10)
C.(8, ![]() )
)
D.( ![]() ,10)
,10)
【答案】C
【解析】解:∵f(x)=log2x,x∈(4,8),
设log2x=t,t∈(2,3),
∵f(x2)=log2x2=2log2x,
∴y=2t+ ![]() =2(t+
=2(t+ ![]() ),
),
设t1 , t2∈(2,3),且t1<t2 ,
∴f(t1)﹣f(t2)=2[(t1+ ![]() )﹣(t2+
)﹣(t2+ ![]() )]=2(t1﹣t2)
)]=2(t1﹣t2) ![]() ,
,
∵t1 , t2∈(2,3),且t1<t2 ,
∴t1﹣t2<0,t1t2﹣4>0,
∴f(t1)﹣f(t2)<0,
∴函数y=f(t)在(2,3)上为增函数,
∴f(2)<y<f(3),
∴8<y< ![]()
∴函数y=f(x2)+ ![]() =2log2x的值域为(8,
=2log2x的值域为(8, ![]() ),
),
故选C.
【考点精析】利用函数单调性的性质和复合函数单调性的判断方法对题目进行判断即可得到答案,需要熟知函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x<﹣4,或x>1},B={x|﹣3≤x﹣1≤2},
(1)求A∩B、(UA)∪(UB);
(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f( ![]() )=
)= ![]() ,则不等式f(t﹣1)+f(t)<0的解集为( )
,则不等式f(t﹣1)+f(t)<0的解集为( )
A.(0,1)
B.(0, ![]() ]
]
C.(0, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)令![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象.区间
的图象.区间![]() 满足:
满足:![]() 在
在![]() 上至少含有30个零点.在所有满足上述条件的
上至少含有30个零点.在所有满足上述条件的![]() 中,求
中,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,试估计该校学生每周平均体育运动时间超过4小时的概率.
,试估计该校学生每周平均体育运动时间超过4小时的概率.
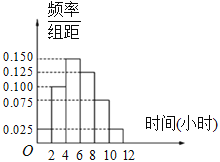
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时.请完成每周平均体育运动时间与性别的列联表,并判断能否在犯错误的概率不超过0.05的前提下认为该校学生的每周平均体育运动时间与性别有关?
男生 | 女生 | 合计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
合计 | 300 |
附:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程x2+ax+2b=0的一个根在(0,1)内,另一个根在(1,2)内,则 ![]() 的取值范围是( )
的取值范围是( )
A.[﹣2,1)
B.(﹣2,1)
C.(﹣∞,﹣2)∪(1,+∞)
D.(﹣∞,﹣2]∪[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)两个共轭复数的差是纯虚数;(2)两个共轭复数的和不一定是实数;(3)若复数a+bi(a,b∈R)是某一元二次方程的根,则a﹣bi是也一定是这个方程的根;(4)若z为虚数,则z的平方根为虚数,
其中正确的个数为( )
A.3
B.2
C.1
D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com