练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线：的焦点为，抛物线上的点到准线的最小距离为2.

    （1）求抛物线的方程；

    （2）若过点作互相垂直的两条直线，，与抛物线交于，两点，与抛物线交于，两点，，分别为弦，的中点，求的最小值.

    【答案】（1）；（2）32.

    【解析】

    （1）根据题意，解得答案.

    （2）设直线的斜率为，则直线的斜率为，联立方程解得，，则，利用均值不等式得到答案.

    （1）因为抛物线上的点到准线的最小距离为2，所以，解得，

    故抛物线的方程为.

    （2）焦点为，，所以两直线，的斜率都存在且均不为0.

    设直线的斜率为，则直线的斜率为，

    故直线的方程为，联立方程组

    消去，整理得.

    设点.，则.

    因为为弦的中点，所以.

    由，得，故点.

    同理可得.

    故，.

    所以，当且仅当，即时，等号成立.

    所以的最小值为32.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，点在椭圆上，焦点为，圆O的直径为．

    （1）求椭圆C及圆O的标准方程；

    （2）设直线l与圆O相切于第一象限内的点P，且直线l与椭圆C交于两点．记 的面积为，证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

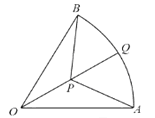
    【题目】如图，三个校区分别位于扇形OAB的三个顶点上，点Q是弧AB的中点，现欲在线段OQ上找一处开挖工作坑P（不与点O，Q重合），为小区铺设三条地下电缆管线PO，PA，PB，已知OA＝2千米，∠AOB＝，记∠APQ＝θrad，地下电缆管线的总长度为y千米．

    （1）将y表示成θ的函数，并写出θ的范围；

    （2）请确定工作坑P的位置，使地下电缆管线的总长度最小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，圆经过伸缩变换后得到曲线．以坐标原点为极点，轴的正半轴为极轴，并在两种坐标系中取相同的单位长度，建立极坐标系，直线的极坐标方程为．

    （1）求曲线的直角坐标方程及直线的直角坐标方程；

    （2）设点是上一动点，求点到直线的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题，拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度，责成人社部进行调研.人社部从网上年龄在15∽65岁的人群中随机调查100人，调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下：

    年龄

    支持“延迟退休”的人数

    15

    5

    15

    28

    17

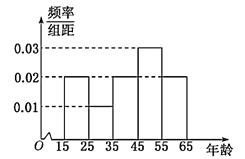
    （1）由以上统计数据填列联表，并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异；

    45岁以下

    45岁以上

    总计

    支持

    不支持

    总计

    （2）若以45岁为分界点，从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人

    ①抽到1人是45岁以下时，求抽到的另一人是45岁以上的概率.

    ②记抽到45岁以上的人数为，求随机变量的分布列及数学期望.

    参考数据：

    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    ，其中

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求证：；

    （2）讨论函数零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知半径为的球面上有两点，且，球心为，若是球面上的动点，且二面角的大小为，则四面体的外接球表面积为______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在四棱锥中,底面为平行四边形, 为侧棱的中点.

    （Ⅰ）求证: ∥平面

    （Ⅱ）若,,

    求证:平面平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位对员工业务进行考核，从类员工(工作3年及3年以内的员工)和类员工(工作3年以上的员工)的成绩中各抽取15个，具体数据如下：

    类成绩：20 10 22 30 15 12 41 22 31 25 12 26 29 32 33

    类成绩：21 40 30 41 42 31 49 51 52 43 47 47 32 45 48

    （1）根据两组数据完成两类员工成绩的茎叶图，并通过茎叶图比较两类员工成绩的平均值及分散程度(不要求计算出具体值，得出结论即可)；

    （2）研究发现从业时间与业务能力之间具有线性相关关系，从上述抽取的名员工中抽取4名员工的成绩如下：

    员工工作时间(单位年)

    1

    2

    3

    4

    考核成绩

    10

    15

    20

    30

    根据四个的数据，求关于的线性回归方程．

    附：回归直线的斜率和截距的最小二乘法估计公式分别为：，．

    查看答案和解析>>

    同步练习册答案