
【题目】设函数![]()
![]() .若曲线
.若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先根据导数几何意义得![]() ,再由
,再由![]() ,解得
,解得![]() .最后求出导函数零点,列表分析导函数符号变号规律,进而确定单调区间,(2)先分离
.最后求出导函数零点,列表分析导函数符号变号规律,进而确定单调区间,(2)先分离![]() ,再求函数
,再求函数![]() 最大值,即得实数
最大值,即得实数![]() 的取值范围.
的取值范围.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() .
.
![]() .
.
依题意得![]() ,
, ![]() ,即
,即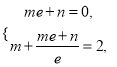
所以![]() .
.
所以![]() ,
, ![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)设函数![]() ,故对任意
,故对任意![]() ,不等式
,不等式![]() 恒成立.
恒成立.
又![]() ,当
,当![]() ,即
,即![]() 恒成立时,
恒成立时,
函数![]() 单调递减,设
单调递减,设![]() ,则
,则![]() ,
,
所以![]() ,即
,即![]() ,符合题意;
,符合题意;
当![]() 时,
时, ![]() 恒成立,此时函数
恒成立,此时函数![]() 单调递增.
单调递增.
于是,不等式![]() 对任意
对任意![]() 恒成立,不符合题意;
恒成立,不符合题意;
当![]() 时,设
时,设![]() ,
,
则![]()
![]() ;
;
当![]() 时,
时, ![]() ,此时
,此时![]() 单调递增,
单调递增,
所以![]()
![]() ,
,
故当![]() 时,函数
时,函数![]() 单调递增.
单调递增.
于是当![]() 时,
时, ![]() 成立,不符合题意;
成立,不符合题意;
综上所述,实数![]() 的取值范围为:
的取值范围为: ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地抽查产品进行检测,现在某条生产线上随机抽取100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.

(1)求图中![]() 的值;
的值;
(2)求综合评分的中位数;
(3)用样本估计总体,以频率作为概率,按分层抽样的思想,先在该条生产线中随机抽取5个产品,再从这5个产品中随机抽取2个产品记录有关数据,求这2个产品中至多有一个一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台为宣传本市,随机对本市内![]() 岁的人群抽取了
岁的人群抽取了![]() 人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |

(1)分别求出![]() 的值;
的值;
(2)根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数;
(3)若第1组回答正确的人员中,有2名女性,其余为男性,现从中随机抽取2人,求至少抽中1名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海中一小岛![]() 的周围
的周围![]()
![]() 内有暗礁,海轮由西向东航行至
内有暗礁,海轮由西向东航行至![]() 处测得小岛
处测得小岛![]() 位于北偏东
位于北偏东![]() ,航行8
,航行8![]() 后,于
后,于![]() 处测得小岛
处测得小岛![]() 在北偏东
在北偏东![]() (如图所示).
(如图所示).

(1)如果这艘海轮不改变航向,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘海轮在![]() 处改变航向为东偏南
处改变航向为东偏南![]() (
(![]() )方向航行,求
)方向航行,求![]() 的最小值.
的最小值.
附: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口的水深![]() (米)是时间
(米)是时间![]() (
(![]() ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 10 | 13 | 9.9 | 7 | 10 | 13 | 10.1 | 7 | 10 |
经过长期观测, ![]() 可近似的看成是函数
可近似的看成是函数![]()
(1)根据以上数据,求出![]() 的解析式
的解析式
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中几个小时可以安全的进出该港?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)若函数f(x)的图像中相邻两条对称轴间的距离不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若函数f(x)的最小正周期为π,且当x∈![]() 时,f(x)的最大值是
时,f(x)的最大值是![]() ,求函数f(x)的最小值,并说明如何由函数y=sin2x的图象变换得到函数y=f(x)的图象.
,求函数f(x)的最小值,并说明如何由函数y=sin2x的图象变换得到函数y=f(x)的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市在2018年元旦举办了一次抽奖活动,抽奖箱里放有2个红球,1个黄球和1个蓝球(这些小球除颜色外大小形状完全相同),从中随机一次性取2个小球,每位顾客每次抽完奖后将球放回抽奖箱.活动另附说明如下:
①凡购物满100(含100)元者,凭购物打印凭条可获得一次抽奖机会;
②凡购物满188(含188)元者,凭购物打印凭条可获得两次抽奖机会;
③若取得的2个小球都是红球,则该顾客中得一等奖,奖金是一个10元的红包;
④若取得的2个小球都不是红球,则该顾客中得二等奖,奖金是一个5元的红包;
⑤若取得的2个小球只有1个红球,则该顾客中得三等奖,奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据(单位:元),绘制得到如图所示的茎叶图.

(1)求这20位顾客中获得抽奖机会的人数与抽奖总次数(假定每位获得抽奖机会的顾客都会去抽奖);
(2)求这20位顾客中奖得抽奖机会的顾客的购物消费数据的中位数与平均数(结果精确到整数部分);
(3)分别求在一次抽奖中获得红包奖金10元,5元,2元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,m,n表示两条不同的直线,![]() 、
、![]() 、
、![]() 表示三个不同的平面.正确的命题是( )
表示三个不同的平面.正确的命题是( )
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 若
若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com