
【题目】已知在锐角![]() 中,角
中,角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,且
,且![]()
(1)求角![]() 大小;
大小;
(2)当![]() 时,求
时,求![]() 的取值范围。
的取值范围。
【答案】(1)由已知及余弦定理,得![]() 因为
因为![]() 为锐角,所以
为锐角,所以![]()
(2)由正弦定理,得![]() ,
,
![]()
![]()
![]()
由![]() 得
得![]()
![]()
![]()
【解析】
试题分析:(I)利用锐角△ABC中,sinC=![]() ,求出角C的大小;(II)先求得 B+A=150°,根据B、A都是锐角求出A的范围,由正弦定理得到a=2sinA,b=2sinB=2sin(A+30°),根据 a2+b2=4+2
,求出角C的大小;(II)先求得 B+A=150°,根据B、A都是锐角求出A的范围,由正弦定理得到a=2sinA,b=2sinB=2sin(A+30°),根据 a2+b2=4+2![]() sin(2A﹣60°) 及A的范围,得(2A﹣60°),从而得到a2+b2的范围.
sin(2A﹣60°) 及A的范围,得(2A﹣60°),从而得到a2+b2的范围.
详解:(I)由已知及余弦定理,得tanC=![]() =
=![]() =
=![]() ,
,
∴sinC=![]() ,故锐角C=
,故锐角C=![]() .
.
(II)当C=1时,∵B+A=150°,∴B=150°﹣A.由题意得![]() ,
,
∴60°<A<90°.由 ![]() =2,得 a=2sinA,b=2sinB=2sin(A+30°),
=2,得 a=2sinA,b=2sinB=2sin(A+30°),
∴a2+b2=4[sin2A+sin2(A+30°)]=4[![]() +
+![]() ]=4[1﹣
]=4[1﹣![]() cos2A﹣
cos2A﹣![]() (
(![]() cosA﹣
cosA﹣![]() sin2A)]=4+2
sin2A)]=4+2![]() sin(2A﹣60°).
sin(2A﹣60°).
∵60°<A<90°,∴(2A﹣60°).
∴7<a2+b2≤4+2![]() .
.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校因为寒假延期开学,根据教育部停课不停学的指示,该学校组织学生线上教学,高一年级在线上教学一个月后,为了了解线上教学的效果,在线上组织数学学科考试,随机抽取50名学生(满分150分,且抽取的学生成绩都在![]() 内)的成绩并制成频率分布直方图如图所示.
内)的成绩并制成频率分布直方图如图所示.

(1)根据频率分布直方图,估计这50名同学的数学平均成绩;(同一组中的数据以该组区间的中点值作代表)
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学的数学成绩在同一组中的概率.
的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学的数学成绩在同一组中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 |
|
|
|
|
|
|
|
年利润增长 |
|
|
|
|
|
|
|
(1)请用最小二乘法求出![]() 关于
关于![]() 的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额为
的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额为![]() 万元,估计该公司在该年的年利润增长为多少?(结果保留两位小数)
万元,估计该公司在该年的年利润增长为多少?(结果保留两位小数)
(2)现从2012年—2018年这![]() 年中抽出三年进行调查,记
年中抽出三年进行调查,记![]() 年利润增长
年利润增长![]() 投资金额,设这三年中
投资金额,设这三年中![]() (万元)的年份数为
(万元)的年份数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考公式: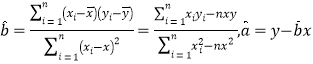 .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两个不同的平面,则
是两个不同的平面,则![]() 的必要不充分条件是( )
的必要不充分条件是( )
A.![]() 内存在一条直线垂直于
内存在一条直线垂直于![]() 内的两条相交直线
内的两条相交直线
B.平行于![]() 的一个平面与
的一个平面与![]() 垂直
垂直
C.![]() 内存在一条直线垂直于
内存在一条直线垂直于![]() 内的无数条直线
内的无数条直线
D.垂直于![]() 的一条直线与
的一条直线与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设L、M、N分别为![]() 的∠BAC、∠ CBA、∠ ACB内的点,且∠BAL=∠ ACL,∠ LBA=∠ LAC,∠ CBM=∠ BAM,∠ MCB=∠ MBA,∠ ACN=∠ CBN,∠ NAC=∠ NCB.
的∠BAC、∠ CBA、∠ ACB内的点,且∠BAL=∠ ACL,∠ LBA=∠ LAC,∠ CBM=∠ BAM,∠ MCB=∠ MBA,∠ ACN=∠ CBN,∠ NAC=∠ NCB.
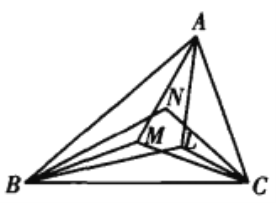
证明:(1) AL、BM、CN三线交于一点P;
(2)L、M、N、P四点共圆.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com