
【题目】已知关于x,y的方程x2+y2﹣4x+4y+m=0表示一个圆.
(1)求实数m的取值范围;
(2)若m=4,过点P(0,2)的直线l与圆相切,求出直线l的方程.
【答案】(1) m<8.(2)![]() 和x=0.
和x=0.
【解析】
(1)可配方,方程左边是平方和形式,右边为正即可;
(2)斜率不存在时,直线![]() 是圆的切线,斜率存在时,设方程为
是圆的切线,斜率存在时,设方程为![]() ,由圆心到切线距离等于半径可求得
,由圆心到切线距离等于半径可求得![]() ,得切线方程.
,得切线方程.
(1)方程x2+y2﹣4x+4y+m=0可化为(x﹣2)2+(y+2)2=8﹣m,
令8﹣m>0,解得m<8;
所以方程表示圆时m的取值范围是m<8.
(2)m=4时,圆的方程为(x﹣2)2+(y+2)2=4,
则圆心为C(2,﹣2),半径为r=2,
当直线l的斜率k存在时,设l的方程为:y=kx+2,
化为kx﹣y+2=0,
则圆心C到直线l的距离为d![]() 2,解得k
2,解得k![]() ,
,
所以直线l的方程为y![]() x+2;
x+2;
当直线l的斜率k不存在时,直线x=0也为圆C的切线;
综上,直线l的方程为![]() 和x=0.
和x=0.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足: ![]() ,
, 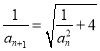 ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,试确定
,试确定![]() 的值,使得数列
的值,使得数列![]() 为等差数列;
为等差数列;
(3)将数列![]() 中的部分项按原来顺序构成新数列
中的部分项按原来顺序构成新数列![]() ,且
,且![]() ,求证:存在无数个满足条件的无穷等比数列
,求证:存在无数个满足条件的无穷等比数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,证明直线
,证明直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .若直线
.若直线![]() 上存在点P,使得
上存在点P,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,求直线
为顶角的等腰直角三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上海市普通高中学业水平等级考成绩共分为五等十一级,各等级换算成分数如表所示:
等级 |
| A |
| B |
|
| C |
|
| D | E |
分数 | 70 | 67 | 64 | 61 | 58 | 55 | 52 | 49 | 46 | 43 | 40 |
上海某高中2018届高三![]() 班选考物理学业水平等级考的学生中,有5人取得
班选考物理学业水平等级考的学生中,有5人取得![]() 成绩,其他人的成绩至少是B级及以上,平均分是64分,这个班级选考物理学业水平等级考的人数至少为______人
成绩,其他人的成绩至少是B级及以上,平均分是64分,这个班级选考物理学业水平等级考的人数至少为______人![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的等边三角形,上、下底面的面积之比为
的等边三角形,上、下底面的面积之比为![]() ,侧面
,侧面![]() 底面
底面![]() ,并且
,并且![]() .
.
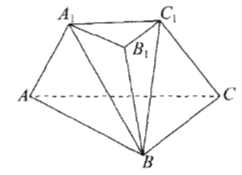
(1)平面![]() 平面
平面![]() ,证明:
,证明:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com