
【题目】已知f(x)=x3﹣ax在(﹣∞,﹣1]上是单调函数,则a的取值范围是( )
A.(3,+∞)
B.[3,+∞)
C.(﹣∞,3)
D.(﹣∞,3]
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:f′(x)>1﹣f(x),f(0)=6,f′(x)是f(x)的导函数,则不等式 ![]() (其中e为自然对数的底数)的解集为( )
(其中e为自然对数的底数)的解集为( )
A.(0,+∞)
B.(﹣∞,0)∪(3,+∞)
C.(﹣∞,0)∪(1,+∞)
D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4个不同的球,4个不同的盒子,把球全部放入盒子内.
(1)共有几种放法?
(2)恰有1个空盒,有几种放法?
(3)恰有2个盒子不放球,有几种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题: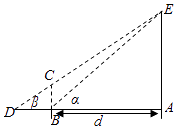
(1)若测得α=60°、β=30°,试求H的值;
(2)经过分析若干次测得的数据后,大家一致认为适当调整标杆到树木的距离d(单位:m),使α与β之差较大时,可以提高测量精确度.
若树木的实际高度为8m,试问d为多少时,α﹣β最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,且△ABC为等边三角形,AA1=AB=6,D为AC的中点.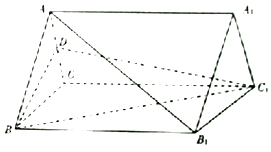
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面ACC1A1;
(3)求三棱锥C﹣BC1D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知正方体ABCD-A1B1C1D1.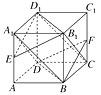
(1)求证:平面A1BD∥平面B1D1C.
(2)若E , F分别是AA1 , CC1的中点,求证:平面EB1D1∥平面FBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx
(1)求f(x)在点(1,f(1))处的切线方程;
(2)若函数 ![]() 在[1,e]上的最小值为
在[1,e]上的最小值为 ![]() ,求a的值;
,求a的值;
(3)若k∈Z,且f(x)+x﹣k(x﹣1)>0对任意x>1恒成立,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com