
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)对![]() a∈(0,1),是否存在实数λ,
a∈(0,1),是否存在实数λ,![]() ,使
,使![]() 成立,若存在,求λ的取值范围;若不存在,请说明理由.
成立,若存在,求λ的取值范围;若不存在,请说明理由.
【答案】(1)答案不唯一见解析(2)存在,![]() .
.
【解析】
(1)求函数导数,分![]() 三种情况,分析
三种情况,分析![]() 与
与![]() 的关系,即可求出函数的单调区间;
的关系,即可求出函数的单调区间;
(2)由题意转化为![]() 且
且![]() ,利用导数求出
,利用导数求出![]() ,
,![]() ,即转化为
,即转化为![]() ,构造函数
,构造函数![]() ,利用导数可求出
,利用导数可求出![]() ,即可求解.
,即可求解.
(1)![]()
![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
①当a=0时,![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
②当a>0时,![]() ,
, ![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
③当a<0时,![]() ,
,
![]()
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)由![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,故当
,故当![]() 时,
时,![]()
当![]() 时,
时,![]() ,由(1)知,当
,由(1)知,当![]() 时,
时,![]()
所以![]() ,
,
若对![]() 使
使![]() 成立,即
成立,即![]()
则![]() 且
且![]() .
.
所以![]() ,所以
,所以 ![]() .
.
设![]() ,则
,则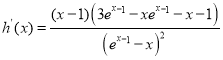 ,
,
令![]() 则
则![]() ,
,
当![]() 时,由
时,由![]() ,故
,故![]() ,
,
所以![]() ,故
,故![]() ,
,
所以![]() 在[0,1]上单调递减,
在[0,1]上单调递减,
所以![]() 时,
时,![]() ,即
,即![]() ,
,
又![]() 时,
时, ![]() ,
,
所以当![]() 时,
时,![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() ,
,
即![]() 时,
时,![]() ,故
,故![]() .
.
所以当![]() 时,对
时,对![]()
使![]() 成立.
成立.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】定义:若向量列![]() ,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即
,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即![]() (
(![]() ,且
,且![]() ,
,![]() 为常向量),则称这个向量列
为常向量),则称这个向量列![]() 为等差向量列,这个常向量叫做等差向量列的公差,且向量列
为等差向量列,这个常向量叫做等差向量列的公差,且向量列![]() 的前
的前![]() 项和为
项和为![]() .已知等差向量列
.已知等差向量列![]() 满足
满足![]() ,则向量列
,则向量列![]() 的前
的前![]() 项和
项和![]() ( )
( )
A.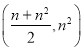 B.
B.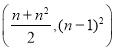
C.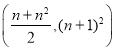 D.
D.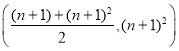
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知衡量病毒传播能力的最重要指标叫做传播指数RO.它指的是,在自然情况下(没有外力介入,同时所有人都没有免疫力),一个感染到某种传染病的人,会把疾病传染给多少人的平均数.它的简单计算公式是:![]() 确认病例增长率
确认病例增长率![]() 系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确认病例的平均增长率为
系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确认病例的平均增长率为![]() ,两例连续病例的间隔时间的平均数为
,两例连续病例的间隔时间的平均数为![]() 天,根据以上RO数据计算,若甲得这种传染病,则
天,根据以上RO数据计算,若甲得这种传染病,则![]() 轮传播后由甲引起的得病的总人数约为( )
轮传播后由甲引起的得病的总人数约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月,某公司以问卷的形式调查影响员工积极性的六项关键指标:绩效奖励、排班制度、激励措施、工作环境、人际关系、晋升渠道,在确定各项指标权重结果后,进而得到指标重要性分析象限图(如图).若客户服务中心从中任意抽取不同的两项进行分析,则这两项来自影响稍弱区的概率为( )
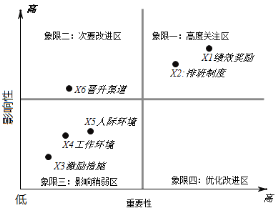
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com