
ЁОЬтФПЁПЫцзХЮвЙњОгУёЩњЛюЫЎЦНЕФВЛЖЯЬсИпЃЌЦћГЕж№ВННјШыАйаеМвЭЅЃЌЕЋЫцжЎУцРДЕФНЛЭЈгЕЖТКЭНЛЭЈЪТЙЪЪБгаЗЂЩњЃЌИјШЫУёЕФЩњЛювВДјРДСЫжюЖрВЛБуЃЎФГЪаЮЊСЫШЗБЃНЛЭЈАВШЋЃЎОіЖЈЖдНЛЭЈжШађзіНјВНећЖйЃЌЖддкЭЈТЗЩЯааЪЛЕФЧАКѓЯрСкСНЛњЖЏГЕжЎМфЕФОрРыdЃЈУзЃЉгыЛњЖЏГЕааЪЛЫйЖШvЃЈЧЇУз/аЁЪБЃЉзіГіШчЯТСНЬѕЙцЖЈЃК
Ђй![]() av2ЃЛ
av2ЃЛ
Ђк![]() ЃЎЃЈЦфжаaЪЧГЃСПЃЌБэЪОГЕЩэГЄЖШЃЌЕЅЮЛЃКУзЃЉ
ЃЎЃЈЦфжаaЪЧГЃСПЃЌБэЪОГЕЩэГЄЖШЃЌЕЅЮЛЃКУзЃЉ
ЃЈ1ЃЉЕБ![]() ЪБЃЎЧѓЛњЖЏГЕЕФзюДѓааЪЛЫйЖШЃЛ
ЪБЃЎЧѓЛњЖЏГЕЕФзюДѓааЪЛЫйЖШЃЛ
ЃЈ2ЃЉЩшЛњЖЏГЕУПаЁЪБСїСПQ![]() ЃЌЮЪЕБЛњЖЏГЕааЪЛЫйЖШvЁн30ЃЈЧЇУз/аЁЪБЃЉЪБЃЌЛњЖЏГЕвдЪВУДбљЕФзДЬЌааЪЛЃЌФмЪЙЛњЖЏГЕУПаЁЪБСїСПQзюДѓЃПВЂЫЕУїРэгЩЃЎЃЈЛњЖЏГЕУПаЁЪБСїСПQЪЧжИУПаЁЪБЭЈЙ§ЙлВтЕуЕФГЕСОЪ§ЃЉ
ЃЌЮЪЕБЛњЖЏГЕааЪЛЫйЖШvЁн30ЃЈЧЇУз/аЁЪБЃЉЪБЃЌЛњЖЏГЕвдЪВУДбљЕФзДЬЌааЪЛЃЌФмЪЙЛњЖЏГЕУПаЁЪБСїСПQзюДѓЃПВЂЫЕУїРэгЩЃЎЃЈЛњЖЏГЕУПаЁЪБСїСПQЪЧжИУПаЁЪБЭЈЙ§ЙлВтЕуЕФГЕСОЪ§ЃЉ
ЁОД№АИЁПЃЈ1ЃЉ20![]() ЧЇУз/аЁЪБЃЛЃЈ2ЃЉvЃН40ЪБЃЌQШЁзюДѓжЕЃЌМћНтЮі
ЧЇУз/аЁЪБЃЛЃЈ2ЃЉvЃН40ЪБЃЌQШЁзюДѓжЕЃЌМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтЃЌЕУ![]() ЃЌНтВЛЕШЪНМДПЩЕУЕНБОЬтД№АИЃЛ
ЃЌНтВЛЕШЪНМДПЩЕУЕНБОЬтД№АИЃЛ
ЃЈ2ЃЉИљОнdТњзуЕФВЛЕШЪНЃЌвдзюаЁГЕОрДњЬцdЃЌЧѓДЫЪБQЕФзюжЕМДПЩ.
ЃЈ1ЃЉгЩЬтЃЌЕУ![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЫљвдЛњЖЏГЕЕФзюДѓааЪЛЫйЖШЮЊ![]() ЧЇУз/аЁЪБЃЛ
ЧЇУз/аЁЪБЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ 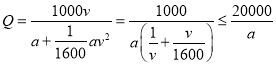 ЃЌ
ЃЌ
ЕБЧвНіЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌQШЁзюДѓжЕЮЊ
ЪБЃЌQШЁзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
ЫљвдЕБЛњЖЏГЕвд40ЃЈЧЇУз/аЁЪБЃЉааЪЛЃЌФмЪЙЛњЖЏГЕУПаЁЪБСїСПQзюДѓЃЌзюДѓжЕЮЊ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшf(x)ЪЧЖЈвхдкR ЧвжмЦкЮЊ1ЕФКЏЪ§ЃЌдкЧјМф![]() ЩЯЃЌ
ЩЯЃЌ ![]() ЦфжаМЏКЯD=
ЦфжаМЏКЯD=![]() ЃЌдђЗНГЬf(x)-lgx=0ЕФНтЕФИіЪ§ЪЧ____________
ЃЌдђЗНГЬf(x)-lgx=0ЕФНтЕФИіЪ§ЪЧ____________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЯрНЛгк
ЯрНЛгк![]() СНЕуЃЌ
СНЕуЃЌ![]() ЮЊзјБъдЕуЃЌжБЯп
ЮЊзјБъдЕуЃЌжБЯп![]() гы
гы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЌЧв
ЃЌЧв![]() .
.
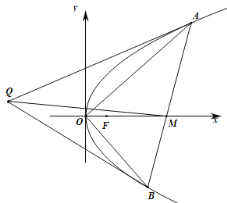
ЃЈ1ЃЉЧѓжЄ:![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЕу![]() ЕФКсзјБъЃЛ
ЕФКсзјБъЃЛ
ЃЈ3ЃЉЙ§![]() ЕуЗжБ№зїХзЮяЯпЕФЧаЯпЃЌСНЬѕЧаЯпНЛгкЕу
ЕуЗжБ№зїХзЮяЯпЕФЧаЯпЃЌСНЬѕЧаЯпНЛгкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаЫЕЗЈЃК
ЂйУќЬтЁАШє![]() ЃЌдђ
ЃЌдђ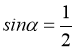 ЁБЕФЗёУќЬтЪЧМйУќЬтЃЛ
ЁБЕФЗёУќЬтЪЧМйУќЬтЃЛ
ЂкУќЬт![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ЂлЁА![]() ЁБЪЧЁАКЏЪ§
ЁБЪЧЁАКЏЪ§![]() ЮЊХМКЏЪ§ЁБЕФГфвЊЬѕМўЃЛ
ЮЊХМКЏЪ§ЁБЕФГфвЊЬѕМўЃЛ
ЂмУќЬт![]() ЁА
ЁА![]() ЃЌЪЙ
ЃЌЪЙ![]() ЁБЃЌУќЬт
ЁБЃЌУќЬт![]() ЁАдк
ЁАдк![]() жаЃЌШє
жаЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ЁБЃЌФЧУДУќЬт
ЁБЃЌФЧУДУќЬт![]() ЮЊецУќЬт.
ЮЊецУќЬт.
Цфжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ fЃЈxЃЉЃНЃЈxЉ1ЃЉexЉax2ЃЎ![]() ЃЎ
ЃЎ
(1)ЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
(2)Шє![]() дк
дк![]() ДІШЁЕУМЋДѓжЕЃЌЧѓ
ДІШЁЕУМЋДѓжЕЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() ЕФСНИіНЙЕуЗжБ№ЮЊ
ЕФСНИіНЙЕуЗжБ№ЮЊ![]() КЭ
КЭ![]() ЃЌЖЬжсЕФСНИіЖЫЕуЗжБ№ЮЊ
ЃЌЖЬжсЕФСНИіЖЫЕуЗжБ№ЮЊ![]() КЭ
КЭ![]() ЃЌЕу
ЃЌЕу![]() дкЭждВ
дкЭждВ![]() ЩЯЃЌЧвТњзу
ЩЯЃЌЧвТњзу![]() ЃЌЕБ
ЃЌЕБ![]() БфЛЏЪБЃЌИјГіЯТСаШ§ИіУќЬтЃК
БфЛЏЪБЃЌИјГіЯТСаШ§ИіУќЬтЃК
ЂйЕу![]() ЕФЙьМЃЙигк
ЕФЙьМЃЙигк![]() жсЖдГЦЃЛЂк
жсЖдГЦЃЛЂк![]() ЕФзюаЁжЕЮЊ2ЃЛ
ЕФзюаЁжЕЮЊ2ЃЛ
ЂлДцдк![]() ЪЙЕУЭждВ
ЪЙЕУЭждВ![]() ЩЯТњзуЬѕМўЕФЕу
ЩЯТњзуЬѕМўЕФЕу![]() НігаСНИіЃЌ
НігаСНИіЃЌ
ЦфжаЃЌЫљгае§ШЗУќЬтЕФађКХЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбјжГГЁашвЊЭЈЙ§ФГзАжУЖдбјжГГЕМфНјааКуЮТПижЦЃЌЮЊСЫНтШегУЕчСП![]() гыШеЦНОљЦјЮТ
гыШеЦНОљЦјЮТ![]() ЃЈЁцЃЉжЎМфЕФЙиЯЕЃЌЫцЛњЭГМЦСЫФГ5ЬьЕФгУЕчСПгыЕБЬьЦНОљЦјЮТЃЌВЂжЦзїСЫЖдееБэЃК
ЃЈЁцЃЉжЎМфЕФЙиЯЕЃЌЫцЛњЭГМЦСЫФГ5ЬьЕФгУЕчСПгыЕБЬьЦНОљЦјЮТЃЌВЂжЦзїСЫЖдееБэЃК
ШеЦНОљЦјЮТЃЈЁцЃЉ | 3 | 4 | 5 | 6 | 7 |
ШегУЕчСПЃЈ | 2.5 | 3 | 4 | 4.5 | 6 |
ЃЈЂёЃЉЧѓ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЃЛ
ЕФЯпадЛиЙщЗНГЬЃЛ
ЃЈЂђЃЉЧыРћгУЃЈЂёЃЉжаЕФЯпадЛиЙщЗНГЬдЄВтШеЦНОљЦјЮТЮЊ12ЁцЪБЕФШегУЕчСП.
ИНЃКЛиЙщжБЯпЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЗЈЙРМЦЙЋЪНЗжБ№ЮЊ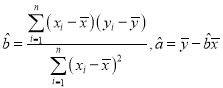 .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЭждВCЃК![]() ЕФгвзМЯпЗНГЬЮЊxЃН4ЃЌгвЖЅЕуЮЊAЃЌЩЯЖЅЕуЮЊBЃЌгвНЙЕуЮЊFЃЌаБТЪЮЊ2ЕФжБЯпlОЙ§ЕуAЃЌЧвЕуFЕНжБЯпlЕФОрРыЮЊ
ЕФгвзМЯпЗНГЬЮЊxЃН4ЃЌгвЖЅЕуЮЊAЃЌЩЯЖЅЕуЮЊBЃЌгвНЙЕуЮЊFЃЌаБТЪЮЊ2ЕФжБЯпlОЙ§ЕуAЃЌЧвЕуFЕНжБЯпlЕФОрРыЮЊ![]() .
.
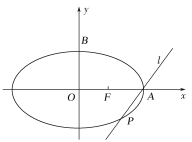
(1)ЧѓЭждВCЕФБъзМЗНГЬЃЎ
(2)НЋжБЯпlШЦЕуAа§зЊЃЌЫќгыЭждВCЯрНЛгкСэвЛЕуPЃЌЕБBЃЌFЃЌPШ§ЕуЙВЯпЪБЃЌЪдШЗЖЈжБЯпlЕФаБТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌ
жаЃЌ![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
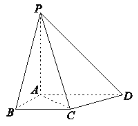
ЃЈ1ЃЉЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкРт![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЦНУц
ЦНУц![]() ЃПШєДцдкЃЌШЗЖЈЕу
ЃПШєДцдкЃЌШЗЖЈЕу![]() ЕФЮЛжУЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФЮЛжУЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com