Question

已知不等式++…+＞［log₂n］,其中n为大于2的整数,［log₂n］表示不超过log₂n的最大整数,设数列{a_n}的各项为正,且满足a₁=?b(b＞0),a_n≤,n=2,3,4,…

(1)证明a_n＜,n=3,4,5,…，

(2)猜测数列{a_n}是否有极限?如果有,写出极限的值(不必证明)；

(3)试确定一个正整数N,使得当n＞N时,对任意b＞0,都有a_n＜.

Answer 1

(1)证法1：∵当n≥2时,0＜a_n≤,

∴≥=+,

即-≥.

于是有-≥,-≥,…,-≥._?

所有不等式两边相加可得_?

-≥++…+._?

由已知不等式知,当n≥3时有,-＞［log₂n］.

∵a₁=b,∴＞+［log₂n］=.

∴a_n＜，n=3,4,5….

证法2:设f(n)=++…+,首先利用数学归纳法证不等式a_n≤,n=3,4,5,….

①当n=3时,

由a₃≤=≤=,知不等式成立.

②假设当n=k(k≥3)时,不等式成立,即a_k≤,

则a_k+1≤=

≤

=

=

=,

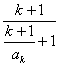
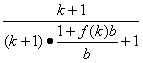
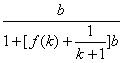
即当n=k+1时,不等式也成立.

由①②知,a_n≤,n=3,4,5,…

又由已知不等式得_?

a_n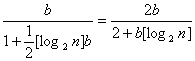＜,n=3,4,5,…

(2)解：有极限,且a_n=0.

(3)解：∵,

令＜,_?

则有log₂n≥［log₂n］＞10n＞2¹⁰=1 024.

故取N=1 024,可使当n＞N时,都有a_n＜.