
 ijʳƷ�ı���ʱ��t����λ��Сʱ���봢���¶�x����λ���棩���㺯����ϵ$t=\left\{\begin{array}{l}64��x��0\\{2^{kx+6}}��x��0.\end{array}\right.$�Ҹ�ʳƷ��4��ı���ʱ����16Сʱ��
ijʳƷ�ı���ʱ��t����λ��Сʱ���봢���¶�x����λ���棩���㺯����ϵ$t=\left\{\begin{array}{l}64��x��0\\{2^{kx+6}}��x��0.\end{array}\right.$�Ҹ�ʳƷ��4��ı���ʱ����16Сʱ������ ����ʳƷ��4��ı���ʱ����16Сʱ�����kֵ��������һ�����ĸ����۵���٣��ɵô𰸣�
��� �⣺��ʳƷ�ı���ʱ��t����λ��Сʱ���봢���¶�x����λ���棩���㺯����ϵ$t=\left\{\begin{array}{l}64��x��0\\{2}^{kx+6}��x��0.\end{array}\right.$�Ҹ�ʳƷ��4��ı���ʱ����16Сʱ��
��24k+6=16����4k+6=4����ã�k=-$\frac{1}{2}$��
��$t=\left\{\begin{array}{l}64��x��0\\{2}^{-\frac{1}{2}x+6}��x��0.\end{array}\right.$��
��x=6ʱ��t=8���ʢٸ�ʳƷ��6��ı���ʱ����8Сʱ����ȷ��
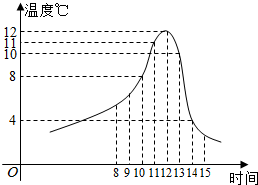
�ڵ�x��[-6��0]ʱ������ʱ���Ϊ64Сʱ����x�ʣ�0��6]ʱ����ʳƷ�ı���ʱ��t�濴x��������٣��ʴ���
�۵��˴���10ʱ���¶ȳ���8�ȣ���ʱ����ʱ�䲻����4Сʱ���ʵ�13ʱ�����������ʳƷ���ڱ���ʱ���ڣ��ʴ���
�ܵ��˴���14ʱ�����������ʳƷ��Ȼ���˱���ʱ�䣬����ȷ��
����ȷ�Ľ��۵����Ϊ���٢ܣ�
�ʴ�Ϊ���٢ܣ�
���� ���������������ж�Ϊ���壬�����˺�����ʵ�������е�Ӧ�ã��Ѷ��е���


 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ${x^2}-\frac{y^2}{4}=1$ | B�� | ${y^2}-\frac{x^2}{4}=1$ | ||
| C�� | $\frac{x^2}{4}-\frac{y^2}{16}=1$����$\frac{y^2}{4}-\frac{x^2}{16}=1$ | D�� | ${x^2}-\frac{y^2}{4}=1$����${y^2}-\frac{x^2}{4}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
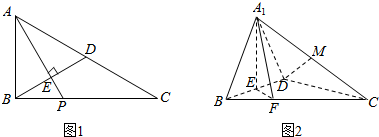
 ��ͼ��������ABCD�ı߳�Ϊ6����E��F�ֱ��ڱ�AD��BC�ϣ���DE=2AE��CF=2BF��������ڳ����ˣ���������ABCD���������ϣ�����ֻ��6����ͬ�ĵ�Pʹ��$\overrightarrow{PE}•\overrightarrow{PF}=��$��������ô�˵�ȡֵ��Χ�ǣ�������
��ͼ��������ABCD�ı߳�Ϊ6����E��F�ֱ��ڱ�AD��BC�ϣ���DE=2AE��CF=2BF��������ڳ����ˣ���������ABCD���������ϣ�����ֻ��6����ͬ�ĵ�Pʹ��$\overrightarrow{PE}•\overrightarrow{PF}=��$��������ô�˵�ȡֵ��Χ�ǣ�������| A�� | ��0��7�� | B�� | ��4��7�� | C�� | ��0��4�� | D�� | ��-5��16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��+�ޣ� | B�� | ��-�ޣ�1�� | C�� | ��-1��+�ޣ� | D�� | ��-�ޣ�-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | 6 | 6 | 9 | 9 |
| �� | 7 | 9 | x | y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com