
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
分析 设A={至少取到两个红球},B={恰好取到一个白球},则AB=B={恰好取到一个白球},由此能求出事件AB的概率.
解答 解:已有3个红球、2个白球的袋中任取3个球,
基本事件总数n=${C}_{5}^{3}$=10,
设A={至少取到两个红球},B={恰好取到一个白球},
则AB=B={恰好取到一个白球},
P(AB)=P(B)=$\frac{{C}_{3}^{2}{C}_{2}^{1}}{{C}_{5}^{3}}$=$\frac{6}{10}$=$\frac{3}{5}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意两个事件同时发生的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 曲线C上的所有点都是“二中点” | |
| B. | 曲线C上的仅有有限个点是“二中点” | |
| C. | 曲线C上的所有点都不是“二中点” | |
| D. | 曲线C上的有无穷多个点(但不是所有的点)是“二中点” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
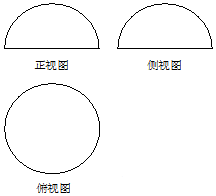 如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )
如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4] | B. | [$\frac{1}{2}$,1) | C. | (1,2] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,CA=CB=$\frac{1}{2}$CC1,点D是棱AA1的中点,且C1D⊥BD
如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,CA=CB=$\frac{1}{2}$CC1,点D是棱AA1的中点,且C1D⊥BD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
如图所示,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com