
【题目】已知函数![]() ,且
,且![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,当
,当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)求极值,可先求得导数![]() ,然后通过解不等式
,然后通过解不等式![]() 确定增区间,解不等式
确定增区间,解不等式![]() 确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记
确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记![]() ,求出其导数
,求出其导数![]() ,可知
,可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() ,这是
,这是![]() 时最小值,
时最小值,![]() ,这是
,这是![]() 时的最大值,因此要证明题中不等式,可分类,
时的最大值,因此要证明题中不等式,可分类,![]() 和
和![]() 分别证明.
分别证明.
试题解析:(1)依题意,![]() ,
,
故![]() ,
,
令![]() ,则
,则![]() 或
或![]() ; 令
; 令![]() ,则
,则![]() ,
,
故当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,当
,当![]() 时,函数
时,函数![]() 有极小值
有极小值![]()
(2)由(1)知![]() ,令
,令![]() ,
,
则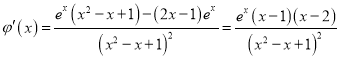 ,
,
可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,令
上单调递减,令![]() .
.
① 当![]() 时,
时,![]() ,所以函数
,所以函数![]() 的图象在
的图象在![]() 图象的上方.
图象的上方.
② 当![]() 时,函数
时,函数![]() 单调递减,所以其最小值为
单调递减,所以其最小值为![]() 最大值为2,而
最大值为2,而![]() ,所以函数
,所以函数![]() 的图象也在
的图象也在![]() 图象的上方.
图象的上方.
综上可知,当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】下面程序执行后,输出的值为( )
J=1;
A=0;
while J<5
J=J+1;
A=A+J* J;
end
print(%io(2),J);
A. 4 B. 5
C. 54 D. 55
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且
且![]() 为等差数列
为等差数列![]() 的前三项.
的前三项.
(1)求![]() 与数列
与数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和
项和![]() ,试问是否存在正整数
,试问是否存在正整数![]() ,对任意的
,对任意的![]() 使得
使得![]() ?若存在请求出
?若存在请求出![]() 的最大值,若不存在请说明理由.
的最大值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),设其导函数为f′(x),当x∈(-∞,0]时,恒有xf′(x)<f(-x),令F(x)=xf(x),则满足F(3)>F(2x-1)的实数x的取值范围是( )
A(![]() ,2) B(-2,1) C(-1,2) D(-1,
,2) B(-2,1) C(-1,2) D(-1,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】50.6,0.65,log0.55的大小顺序是( )
A.0.65 < log0.65 < 50.6B.0.65 < 50.6< log0.65
C.log0.65 < 50.6 <0.65D.log0.65 <0.65 < 50.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,错误的是( )
A. 平行于同一条直线的两个平面平行
B. 平行于同一个平面的两个平面平行
C. 一个平面与两个平行平面相交,交线平行
D. 一条直线与两个平行平面中的一个相交,则必与另一个相交
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com