
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处导数相等,证明:
处导数相等,证明:![]() 为定值,并求出该定值;
为定值,并求出该定值;
(2)已知对于任意![]() ,直线
,直线![]() 与曲线
与曲线![]() 有唯一公共点,求实数
有唯一公共点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)6;(2)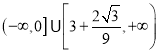
【解析】
(1)求出原函数的导函数,结合在![]() 处导数相等及根与系数的关系可得
处导数相等及根与系数的关系可得![]() ,从而求得
,从而求得![]() 为定值6;(2)由
为定值6;(2)由![]() ,可知函数
,可知函数![]() 在
在![]() 的图象为下凸,在
的图象为下凸,在![]() 的图象为上凸,求得函数的极大值点
的图象为上凸,求得函数的极大值点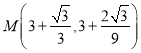 ,再由直线
,再由直线![]() 过点
过点![]() ,然后对
,然后对![]() 分类讨论求使直线
分类讨论求使直线![]() 与曲线
与曲线![]() 有唯一公共点的实数
有唯一公共点的实数![]() 的取值范围.
的取值范围.
(1)证明:![]() ,
,![]() ,
,
由题意得,![]() ,
,
则![]()
![]()
![]()
![]()
![]()
![]() ;
;
(2)解:![]() ,
,
![]() 函数
函数![]() 在
在![]() 的图象为下凸,在
的图象为下凸,在![]() 的图象为上凸,
的图象为上凸,
记![]() ,求得
,求得![]() 处
处![]() 的切线为
的切线为![]() ,再记
,再记![]() ,
,
由![]() ,求得
,求得![]() 的极大值点为
的极大值点为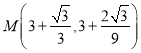 ,
,
①当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 显然只有唯一公共点;
显然只有唯一公共点;
②当![]() 时,直线
时,直线![]() 斜率为正,且与曲线
斜率为正,且与曲线![]() 有三个公共点,舍去;
有三个公共点,舍去;
③当![]() 时,直线
时,直线![]() 斜率为正,且与曲线
斜率为正,且与曲线![]() 有三个公共点,舍去;
有三个公共点,舍去;
④当![]() 时,若
时,若![]() ,
,![]() 在直线上方,直线
在直线上方,直线![]() 与曲线
与曲线![]() 的上凸部分有唯一公共点,与下凸部分不相交;
的上凸部分有唯一公共点,与下凸部分不相交;
若![]() ,直线
,直线![]() 与曲线
与曲线![]() )交于P点,与上凸部分和下凸部分均不相交;
)交于P点,与上凸部分和下凸部分均不相交;
若![]() ,
,![]() 在直线下方,直线y=kx+a与曲线
在直线下方,直线y=kx+a与曲线![]() 的下凸部分有唯一公共点,与上凸部分不相交,此种情况成立.
的下凸部分有唯一公共点,与上凸部分不相交,此种情况成立.
综上,![]() 的取值范围为
的取值范围为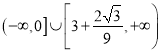 .
.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
①数列![]() 为等差数列的充要条件是其通项公式为n的一次函数.
为等差数列的充要条件是其通项公式为n的一次函数.
②在面积为S的![]() 的边AB上任取一点P,则
的边AB上任取一点P,则![]() 的面积大于
的面积大于![]() 的概率为
的概率为![]() .
.
③将多项式![]() 分解因式得
分解因式得![]() ,则
,则![]() .
.
④若那么由![]() ,那么由
,那么由![]() 以及x轴所围成的图形一定在x轴下方.
以及x轴所围成的图形一定在x轴下方.
其中正确命题的序号为_____________(把所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知过点
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知过点![]() 且斜率为1的直线
且斜率为1的直线![]() 与曲线
与曲线![]() :
:![]() (
(![]() 是参数)交于
是参数)交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() .
.
(1)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 的中点为
的中点为![]() ,比较
,比较![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点,其中直线l不过原点.
两点,其中直线l不过原点.
(1)求椭圆C的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,其中
,其中![]() 且
且![]() .记
.记![]() 的面积为S.分别以
的面积为S.分别以![]() 为直径的圆的面积依次为
为直径的圆的面积依次为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三数学考试中,一般有一道选做题,学生可以从选修4-4和选修4-5中任选一题作答,满分10分.某高三年级共有1000名学生参加了某次数学考试,为了了解学生的作答情况,计划从该年级1000名考生成绩中随机抽取一个容量为10的样本,为此将1000名考生的成绩按照随机顺序依次编号为000~999.
(1)若采用系统抽样法抽样,从编号为000~999的成绩中随机确定的编号为026,求样本中的最大编号.
(2)若采用分层抽样法,按照学生选择选修4-4或选修4-5的情况将成绩分为两层,已知该校共有600名考生选择了选修4-4,400名考生选择了选修4-5,在选取的样本中,选择选修4-4的平均得分为6分,方差为2,选择选修4-5的平均得分为5分,方差为0.75.用样本估计该校1000名考生选做题的平均得分和得分的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,∠ACB=90°,∠ABC=45°,AB=AA1=2,P为CC1的中点.
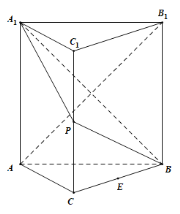
(1)证明:AB1⊥平面PA1B;
(2)设E为BC的中点,线段AB1上是否存在一点Q,使得QE∥平面A1ACC1?若存在,求四棱锥Q﹣AA1C1C的体积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球运动是一项古老的体育活动,众多的资料表明,中国古代足球的出现比欧洲早,历史更为悠久,如图,现代比赛用足球是由正五边形与正六边形构成的共32个面的多面体,著名数学家欧拉证明了凸多面体的面数(F),顶点数(V),棱数(E)满足F+V-E=2,那么,足球有______.个正六边形的面,若正六边形的边长为![]() ,则足球的直径为______.cm(结果保留整数)(参考数据
,则足球的直径为______.cm(结果保留整数)(参考数据![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com