
分析 (Ⅰ)求出f(x)的导数,讨论a<0,a>0,由导数的符号确定单调性,进而得到极值;
(Ⅱ)求出直线AB的斜率kAB,由直线AB与切线平行,得出t与x1+x2的关系式;构造函数g(m),利用函数的单调性证明不等式t<$\frac{{x}_{1}+{x}_{2}}{2}$恒成立即可
解答 解:(Ⅰ)函数f(x)=x-a1nx的导数为f′(x)=1-$\frac{a}{x}$=$\frac{x-a}{x}$,
当a<0时,f′(x)>0,f(x)递增,无极值;
当a>0时,x>a时,f′(x)>0,f(x)递增;0<x<a时,f′(x)<0,f(x)递减.
即有x=a处取得极小值,且为a-alna,无极大值;
综上可得,a<0时,f(x)无极值;
a>0时,f(x)的极小值为a-alna,无极大值;
(Ⅱ)证明:A(x1,y1),B(x2,y2)为曲线y=f(x)上的两个不同点,满足0<x1<x2时,
∴?t∈(x1,x2),使得曲线y=f(x)在x=t处的切线与直线AB平行,
∴kAB=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{{x}_{2}-aln{x}_{2}-({x}_{1}-aln{x}_{1})}{{x}_{2}-{x}_{1}}$
=1-$\frac{a(ln{x}_{2}-ln{x}_{1})}{{x}_{2}-{x}_{1}}$,
又∵f′(x)=1-$\frac{a}{x}$,
∴f(x)在x=t处的切线的斜率为f′(t)=1-$\frac{a}{t}$.
∴1-$\frac{a(ln{x}_{2}-ln{x}_{1})}{{x}_{2}-{x}_{1}}$=1-$\frac{a}{t}$,
即为t=$\frac{{x}_{2}-{x}_{1}}{ln{x}_{2}-ln{x}_{1}}$,
要证t<$\frac{{x}_{1}+{x}_{2}}{2}$,即证$\frac{{x}_{2}-{x}_{1}}{ln{x}_{2}-ln{x}_{1}}$<$\frac{{x}_{1}+{x}_{2}}{2}$,
即为ln$\frac{{x}_{2}}{{x}_{1}}$>2•$\frac{\frac{{x}_{2}}{{x}_{1}}-1}{\frac{{x}_{2}}{{x}_{1}}+1}$,
设$\frac{{x}_{2}}{{x}_{1}}$=m(m>1),
则上述不等式等价于lnm>2•$\frac{m-1}{m+1}$,
即(m+1)lnm>2(m-1);
构造函数g(m)=lnm+$\frac{1}{m}$-1,
当m>1时,g′(m)=$\frac{1}{m}$-$\frac{1}{{m}^{2}}$=$\frac{m-1}{{m}^{2}}$,
∴g′(m)在(1,+∞)上为增函数;
∴g′(m)>g′(1)=0,
∴g(m)在m>1时是增函数,
∴g(m)>g(1)=0;
∴g(m)>0在(1,+∞)上恒成立,
即(m+1)lnm>2(m-1)恒成立.
∴t<$\frac{{x}_{1}+{x}_{2}}{2}$恒成立.
点评 本题考查了利用导数来研究函数的单调性与极值的问题,也考查了利用导数求函数的切线斜率的问题以及不等式的证明问题,是较难的题目.


科目:高中数学 来源: 题型:选择题
| A. | 若直线l平行于平面α内的无数条直线,则l∥α | |
| B. | 若直线a在平面α外,则a∥α | |
| C. | 若直线a∥b,b?α,则a∥α | |
| D. | 若直线a∥b,b?α,则直线a就平行于平面内的无数条直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
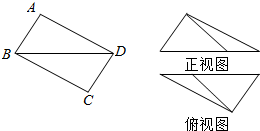 如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )| A. | $\frac{9}{25}$ | B. | $\frac{12}{5}$ | C. | $\frac{18}{25}$ | D. | $\frac{36}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题:| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
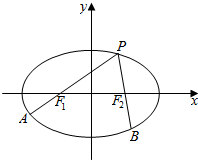 如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )
如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com