
ЁОЬтФПЁПзд2018Фъ10дТ1ШеЦ№ЃЌ![]() жаЛЊШЫУёЙВКЭЙњИіШЫЫљЕУЫА
жаЛЊШЫУёЙВКЭЙњИіШЫЫљЕУЫА![]() аТЙцЖЈЃЌЙЋУёдТЙЄзЪЁЂаНН№ЫљЕУВЛГЌЙ§5000дЊЕФВПЗжВЛБиФЩЫАЃЌГЌЙ§5000дЊЕФВПЗжЮЊШЋдТгІФЩЫАЫљЕУЖюЃЌДЫЯюЫАПюАДЯТБэЗжЖЮРлМЦМЦЫуЃК
аТЙцЖЈЃЌЙЋУёдТЙЄзЪЁЂаНН№ЫљЕУВЛГЌЙ§5000дЊЕФВПЗжВЛБиФЩЫАЃЌГЌЙ§5000дЊЕФВПЗжЮЊШЋдТгІФЩЫАЫљЕУЖюЃЌДЫЯюЫАПюАДЯТБэЗжЖЮРлМЦМЦЫуЃК
ШЋдТгІФЩЫАЫљЕУЖю | ЫАТЪ |
ВЛГЌЙ§1500дЊЕФВПЗж | 3 |
ГЌЙ§1500дЊВЛГЌЙ§4500дЊЕФВПЗж | 10 |
ГЌЙ§4500дЊВЛГЌЙ§9000дЊЕФВПЗж | 20 |
ГЌЙ§9000дЊВЛГЌЙ§35000дЊ | 25 |
|
|
![]() ШчЙћаЁРю10дТЗнШЋдТЕФЙЄзЪЁЂаНН№ЮЊ7000дЊЃЌФЧУДЫћгІИУФЩЫАЖрЩйдЊЃП
ШчЙћаЁРю10дТЗнШЋдТЕФЙЄзЪЁЂаНН№ЮЊ7000дЊЃЌФЧУДЫћгІИУФЩЫАЖрЩйдЊЃП
![]() ШчЙћаЁеХ10дТЗнНЛФЩЫАН№425дЊЃЌФЧУДЫћ10дТЗнЕФЙЄзЪЁЂаНН№ЪЧЖрЩйдЊЃП
ШчЙћаЁеХ10дТЗнНЛФЩЫАН№425дЊЃЌФЧУДЫћ10дТЗнЕФЙЄзЪЁЂаНН№ЪЧЖрЩйдЊЃП
![]() аДГіЙЄзЪЁЂаНН№ЪеШы
аДГіЙЄзЪЁЂаНН№ЪеШы![]() дЊ
дЊ![]() дТ
дТ![]() гыгІНЩФЩЫАН№
гыгІНЩФЩЫАН№![]() дЊ
дЊ![]() ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() дЊЃЛЃЈ3ЃЉ
дЊЃЛЃЈ3ЃЉ
ЁОНтЮіЁП
![]() гЩЗжЖЮРлНјЫМЯыЃЌЯШЫуЕквЛВПЗжЃЌдйЫуЕкЖўВПЗжЃЌМДПЩЕУЕНЫљЧѓжЕЃЛ
гЩЗжЖЮРлНјЫМЯыЃЌЯШЫуЕквЛВПЗжЃЌдйЫуЕкЖўВПЗжЃЌМДПЩЕУЕНЫљЧѓжЕЃЛ![]() ПМТЧЕквЛЖЮ1500дЊЕФЫАЃЌдйПМТЧ3000дЊЕФЫАЃЌНјЖјЫуГіЕкШ§ВПЗжЕФгІНЛЕФЃЌМДПЩЕУЕНЫљЧѓжЕЃЛ
ПМТЧЕквЛЖЮ1500дЊЕФЫАЃЌдйПМТЧ3000дЊЕФЫАЃЌНјЖјЫуГіЕкШ§ВПЗжЕФгІНЛЕФЃЌМДПЩЕУЕНЫљЧѓжЕЃЛ![]() ЗжБ№ПМТЧНЛЫАЕФЧАШ§ВПЗжЃЌдЫгУЗжЖЮРлНјЫМЯыМДПЩЕУЕНЫљЧѓНтЮіЪНЃЎ
ЗжБ№ПМТЧНЛЫАЕФЧАШ§ВПЗжЃЌдЫгУЗжЖЮРлНјЫМЯыМДПЩЕУЕНЫљЧѓНтЮіЪНЃЎ
НтЃК![]() дЊ
дЊ![]() ЃЌ
ЃЌ
гІНЛЫАЮЊ![]() дЊ
дЊ![]() ЃЛ
ЃЛ
![]() аЁеХ10дТЗнНЛФЩЫАН№425дЊЃЌ
аЁеХ10дТЗнНЛФЩЫАН№425дЊЃЌ
гЩЗжЖЮРлНјПЩЕУ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђЫћ10дТЗнЕФЙЄзЪЁЂаНН№ЪЧ![]() дЊЃЛ
дЊЃЛ
![]() ЪБЃЌПЩЕУ
ЪБЃЌПЩЕУ
 ЃЌ
ЃЌ
МДЮЊ ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯТУцЫФИіУќЬтЃК
ЂйЁАШє![]() ЃЌдђ
ЃЌдђ![]() Лђ
Лђ![]() ЁБЕФФцЗёУќЬтЮЊЁАШє
ЁБЕФФцЗёУќЬтЮЊЁАШє![]() Чв
Чв![]() ЃЌдђ
ЃЌдђ![]() ЁБ
ЁБ
ЂкЁА![]() ЁБЪЧЁА
ЁБЪЧЁА![]() ЁБЕФГфЗжВЛБивЊЬѕМў
ЁБЕФГфЗжВЛБивЊЬѕМў
ЂлУќЬтЁАШє![]() ЃЌдђ
ЃЌдђ![]() ЁБЕФФцЗёУќЬтЮЊецУќЬт
ЁБЕФФцЗёУќЬтЮЊецУќЬт
ЂмШє![]() ЮЊМйУќЬтЃЌдђ
ЮЊМйУќЬтЃЌдђ![]() ЁЂ
ЁЂ![]() ОљЮЊМйУќЬтЃЌЦфжаецУќЬтИіЪ§ЮЊЃЈ ЃЉ
ОљЮЊМйУќЬтЃЌЦфжаецУќЬтИіЪ§ЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНAcosЃЈІиx+ІеЃЉЃЈAЃО0ЃЌІиЃО0ЃЌ![]() ІеЃМ0ЃЉЕФЭМЯѓгыyжсЕФНЛЕуЮЊЃЈ0ЃЌ1ЃЉЃЌЫќЕФвЛИізюИпЕуКЭвЛИізюЕЭЕуЕФзјБъЗжБ№ЮЊЃЈx0ЃЌ2ЃЉЃЌЃЈx0
ІеЃМ0ЃЉЕФЭМЯѓгыyжсЕФНЛЕуЮЊЃЈ0ЃЌ1ЃЉЃЌЫќЕФвЛИізюИпЕуКЭвЛИізюЕЭЕуЕФзјБъЗжБ№ЮЊЃЈx0ЃЌ2ЃЉЃЌЃЈx0![]() ЃЌЉ2ЃЉЃЌ
ЃЌЉ2ЃЉЃЌ
ЃЈ1ЃЉШєКЏЪ§fЃЈxЃЉЕФзюаЁе§жмЦкЮЊІаЃЌЧѓКЏЪ§fЃЈxЃЉЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБxЁЪЃЈx0ЃЌx0![]() ЃЉЪБЃЌfЃЈxЃЉЭМЯѓЩЯгаЧвНігавЛИізюИпЕуКЭвЛИізюЕЭЕуЃЌЧвЙигкxЕФЗНГЬfЃЈxЃЉЉaЃН0дкЧјМф[
ЃЉЪБЃЌfЃЈxЃЉЭМЯѓЩЯгаЧвНігавЛИізюИпЕуКЭвЛИізюЕЭЕуЃЌЧвЙигкxЕФЗНГЬfЃЈxЃЉЉaЃН0дкЧјМф[![]() ЃЌ
ЃЌ![]() ]ЩЯгаЧвНігавЛНтЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
]ЩЯгаЧвНігавЛНтЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌШчЭМ1.вд
ЃЌШчЭМ1.вд![]() ЮЊелКлНЋ
ЮЊелКлНЋ![]() елЦ№ЃЌЪЙЕу
елЦ№ЃЌЪЙЕу![]() ЕНДяЕу
ЕНДяЕу![]() ЕФЮЛжУЃЌШчЭМ2.
ЕФЮЛжУЃЌШчЭМ2.
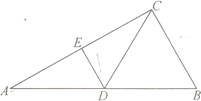

ШчЭМ1 ШчЭМ2
ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕЁЃ
ЫљГЩНЧЕФе§ЯвжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫљИј4ИіЭМЯѓжаЃЌгыЫљИј3МўЪТЮЧКЯзюКУЕФЫГађЮЊ ЃЈ ЃЉ
ЃЈ1ЃЉЮвРыПЊМвВЛОУЃЌЗЂЯжздМКАбзївЕБОЭќдкМвРяСЫЃЌгкЪЧСЂПЬЗЕЛиМвРяШЁСЫзївЕБОдйЩЯбЇЃЛ
ЃЈ2ЃЉЮвГіЗЂКѓЃЌаФЧщЧсЫЩЃЌЛКЛКааНјЃЌКѓРДЮЊСЫИЯЪБМфПЊЪММгЫйЃЛ
ЃЈ3ЃЉЮвЦязХГЕвЛТЗвдГЃЫйааЪЛЃЌжЛЪЧдкЭОжагіЕНвЛДЮНЛЭЈЖТШћЃЌЕЂИщСЫвЛаЉЪБМф.
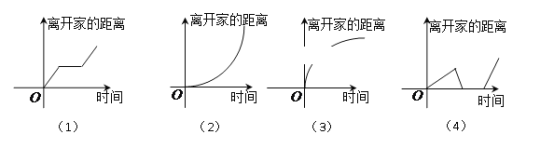
A. ЃЈ1ЃЉЃЈ2ЃЉЃЈ4ЃЉ B. ЃЈ4ЃЉЃЈ2ЃЉЃЈ1ЃЉ C. ЃЈ4ЃЉЃЈ3ЃЉЃЈ1ЃЉ D. ЃЈ4ЃЉЃЈ1ЃЉЃЈ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬте§ШЗЕФЪЧЃЈ ЃЉ
A. УќЬт![]() ЕФЗёЖЈЪЧЃК
ЕФЗёЖЈЪЧЃК![]()
B. УќЬт![]() жаЃЌШє
жаЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ЕФЗёУќЬтЪЧецУќЬт
ЕФЗёУќЬтЪЧецУќЬт
C. ШчЙћ![]() ЮЊецУќЬтЃЌ
ЮЊецУќЬтЃЌ![]() ЮЊМйУќЬтЃЌдђ
ЮЊМйУќЬтЃЌдђ![]() ЮЊецУќЬтЃЌ
ЮЊецУќЬтЃЌ![]() ЮЊМйУќЬт
ЮЊМйУќЬт
D. ![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФзюаЁе§жмЦкЮЊ
ЕФзюаЁе§жмЦкЮЊ![]() ЕФГфЗжВЛБивЊЬѕМў
ЕФГфЗжВЛБивЊЬѕМў
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ10ЗжЃЉЫФУцЬхABCDМАЦфШ§ЪгЭМШчЭМЫљЪОЃЌЦНаагкРтADЃЌBCЕФЦНУцЗжБ№НЛЫФУцЬхЕФРтABЃЌBDЃЌDCЃЌCAгкЕуEЃЌFЃЌGЃЌHЃЎ

ЃЈ1ЃЉЧѓЫФУцЬхABCDЕФЬхЛ§ЃЛ
ЃЈ2ЃЉжЄУїЃКЫФБпаЮEFGHЪЧОиаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬт14ЗжЃЉ
ШчЭМЃЌдкЫФРтзЖP-ABCDжаЃЌЕзУцABCDЮЊОиаЮЃЌЦНУцPADЁЭЦНУцABCDЃЌPAЁЭPDЃЌPA=PDЃЌEЃЌFЗжБ№ЮЊADЃЌPBЕФжаЕу.
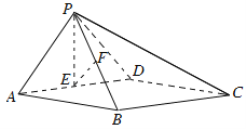
ЃЈЂёЃЉЧѓжЄЃКPEЁЭBCЃЛ
ЃЈЂђЃЉЧѓжЄЃКЦНУцPABЁЭЦНУцPCDЃЛ
ЃЈЂѓЃЉЧѓжЄЃКEFЁЮЦНУцPCD.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЖдШЮвтЕФе§ећЪ§![]() ЃЌзмДцдке§ећЪ§
ЃЌзмДцдке§ећЪ§![]() ЃЌЪЙЕУЪ§Са
ЃЌЪЙЕУЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭ
ЯюКЭ![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЪЧЁАЛиЙщЪ§СаЁБЃЎ
ЪЧЁАЛиЙщЪ§СаЁБЃЎ
ЃЈ![]() ЃЉЂйЧА
ЃЉЂйЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЕФЪ§Са
ЕФЪ§Са![]() ЪЧЗёЪЧЁАЛиЙщЪ§СаЁБЃПВЂЧыЫЕУїРэгЩЃЎЂкЭЈЯюЙЋЪНЮЊ
ЪЧЗёЪЧЁАЛиЙщЪ§СаЁБЃПВЂЧыЫЕУїРэгЩЃЎЂкЭЈЯюЙЋЪНЮЊ![]() ЕФЪ§Са
ЕФЪ§Са![]() ЪЧЗёЪЧЁАЛиЙщЪ§СаЁБЃПВЂЧыЫЕУїРэгЩЃЛ
ЪЧЗёЪЧЁАЛиЙщЪ§СаЁБЃПВЂЧыЫЕУїРэгЩЃЛ
ЃЈ![]() ЃЉЩш
ЃЉЩш![]() ЪЧЕШВюЪ§СаЃЌЪзЯю
ЪЧЕШВюЪ§СаЃЌЪзЯю![]() ЃЌЙЋВю
ЃЌЙЋВю![]() ЃЌШє
ЃЌШє![]() ЪЧЁАЛиЙщЪ§СаЁБЃЌЧѓ
ЪЧЁАЛиЙщЪ§СаЁБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ![]() ЃЉЪЧЗёЖдШЮвтЕФЕШВюЪ§Са
ЃЉЪЧЗёЖдШЮвтЕФЕШВюЪ§Са![]() ЃЌзмДцдкСНИіЁАЛиЙщЪ§СаЁБ
ЃЌзмДцдкСНИіЁАЛиЙщЪ§СаЁБ![]() КЭ
КЭ![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ГЩСЂЃЌЧыИјГіФуЕФНсТлЃЌВЂЫЕУїРэгЩЃЎ
ГЩСЂЃЌЧыИјГіФуЕФНсТлЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com