
【题目】将一个棱长为a的正方体嵌入到四个半径为1且两两相切的实心小球所形成的球间空隙内,使得正方体能够任意自由地转动,则a的最大值为 .
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知 ![]() a=2csinA.
a=2csinA.
(1)求角C的值;
(2)若c= ![]() ,且S△ABC=
,且S△ABC= ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:如图,两同心圆: ![]() 和
和![]() .
. ![]() 为大圆上一动点,连结
为大圆上一动点,连结![]() (
(![]() 为坐标原点)交小圆于点
为坐标原点)交小圆于点![]() ,过点
,过点![]() 作
作![]() 轴垂线
轴垂线![]() (垂足为
(垂足为![]() ),再过点
),再过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() .
.

(1)当点![]() 在大圆上运动时,求垂足
在大圆上运动时,求垂足![]() 的轨迹方程;
的轨迹方程;
(2)过点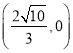 的直线
的直线![]() 交垂足
交垂足![]() 的轨迹于
的轨迹于![]() 两点,若以
两点,若以![]() 为直径的圆与
为直径的圆与![]() 轴相切,求直线
轴相切,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某矿山企业生产某产品的年固定成本为![]() 万元,每生产千件该产品需另投入
万元,每生产千件该产品需另投入![]() 万元,设该企业年内共生产此种产品
万元,设该企业年内共生产此种产品![]() 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为![]() 万元,且
万元,且
(Ⅰ)写出年利润![]() (万元)关于产品年产量
(万元)关于产品年产量![]() (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)问:年产量![]() 为多少千件时,该企业生产此产品所获年利润最大?
为多少千件时,该企业生产此产品所获年利润最大?
注:年利润=年销售收入-年总成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
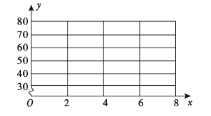
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式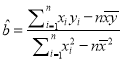 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com