（本小题满分15分）
已知函数
的图象在
上连续不断，定义：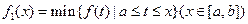 
，
其中，
表示函数在
上的最小值，
表示函数在上的最大值．若存在最小正整数
，使得
对任意的
成立，则称函数为上的“阶收缩函数”．
（1）若
，
，试写出
的表达式；
（2）已知函数
，
，试判断是否为
上的“阶收缩函数”，如果是，求出对应的；如果不是，请说明理由；
（3）已知
，函数
是
上的2阶收缩函数，求
的取值范围.
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
2010年推出一种新型家用轿车，购买时费用为14．4万元，每年应交付保险费．养路费及汽油费共0．7万元，汽车的维修费为：第一年无维修费用，第二年为0．2万元，从第三年起，每年的维修费均比上一年增加0．2万元．
（1）设该辆轿车使用n年的总费用（包括购买费用．保险费．养路费．汽油费及维修费）为f（n），求f（n）的表达式；
（2）这种汽车使用多少年报废最合算（即该车使用多少年，年平均费用最少）？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题12分）
已知函数f(x)=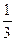
x
－（2a+1）
x
+3a（a+2）x+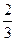
，其中a为实数。
（1）当a=－1时，求函数y=f(x)在[0,6]上的最大值与最小值；
（2）当函数y=f
(x)的图像在（0,6）上与x轴有唯一的公共点时，求实数a的取值范围。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分10分）
小刘家要建造一个长方形无盖蓄水池，其容积为48
，深为3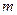
.如果池底每平方米的造价为150元，池壁每平方米的造价为
120元，怎样设计水池能使总造价最低？最低造价是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题12分）已知函数
的图象与x、y轴分别相交于点A、 B，
(
、 
分别是与x、y轴正半轴同方向的单位向量), 函数
(1) 求k、b的值;
(2) 当x满足
时，求函数
的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；(2) 
，
．
为奇函数。且
.（1）求实数
的值。
（－1，1）上是增函数。
。
函数
的定义域为集合
,
(2)
(3) (
的最小值和最小正周期；
的内角
对边分别为
，且
，若
与
共线，求
的值.