
【题目】已知![]() 和
和![]() 。试问:当且仅当
。试问:当且仅当![]() 、
、![]() 满足什么条件时,对
满足什么条件时,对![]() 上任意一点
上任意一点![]() ,均存在以
,均存在以![]() 为顶点、与
为顶点、与![]() 外切、与
外切、与![]() 内接的平行四边形?并证明你的结论。
内接的平行四边形?并证明你的结论。
科目:高中数学 来源: 题型:
【题目】下列命题中正确的命题是( )
A.标准差越小,则反映样本数据的离散程度越大
B.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,则预报变量
每增加1个单位时,则预报变量![]() 减少0.4个单位
减少0.4个单位
C.对分类变量![]() 与
与![]() 来说,它们的随机变量
来说,它们的随机变量![]() 的观测值
的观测值![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大
有关系”的把握程度越大
D.在回归分析模型中,残差平方和越小,说明模型的拟合效果越好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2菱形ABCD中,![]() ,且对角线AC与BD交点为O.沿BD将
,且对角线AC与BD交点为O.沿BD将![]() 折起,使点A到达点
折起,使点A到达点![]() 的位置.
的位置.

(1)若![]() ,求证:
,求证:![]() 平面ABCD;
平面ABCD;
(2)若![]() ,求三棱锥
,求三棱锥![]() 体积.
体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
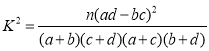 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 作不与
作不与![]() 轴重合的直线
轴重合的直线![]() ,设
,设![]() 与圆
与圆![]() 相交于
相交于![]() 两点,与椭圆相交于
两点,与椭圆相交于![]() 两点,当
两点,当![]() 且
且![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于![]() 的一元二次方程
的一元二次方程![]() .
.
(Ⅰ)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数,![]() 是从
是从![]() 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率.
(Ⅱ)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数,![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四色猜想是近代数学难题之一,四色猜想的内容是:“任何一张地图最多用四种颜色就能使具有共同边界的国家着上不同的颜色”,如图,一张地图被分成了五个区域,每个区域只使用一种颜色,现有4种颜色可供选择(四种颜色不一定用完),则满足四色猜想的不同涂色种数为__________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com