练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，曲线的普通方程为，曲线的参数方程为为参数），以坐标原点为极点， 轴正半轴为极轴建立极坐标系.

    （1）求曲线的极坐标方程；

    （2）求曲线与焦点的极坐标，其中.

    【答案】（1）曲线的极坐标方程为，曲线的极坐标方程为；

    （2）曲线与交点的极坐标.

    【解析】试题分析: （1）根据,可求出的极坐标方程;将消去参数t,可得的普通方程,再利用化简可得的极坐标方程; （2）联立与的普通方程,求出交点坐标,再将交点坐标化为极坐标形式即可.

    试题解析:解：（1）依题意，将代入上式中可得；

    因为，故，将代入上式化简得；

    故曲线的极坐标方程为，曲线的极坐标方程为；

    （2）将代入得，解得（舍去），

    当时， ，所以与交点的平面直角坐标为, ,

    因为，

    所以，故曲线与交点的极坐标.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，若直线的参数方程为（为参数， 为的倾斜角），曲线的极坐标方程为，射线， ， 与曲线分别交于不同于极点的三点.

    （1）求证： ；

    （2）当时，直线过两点，求与的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地政府为了对房地产市场进行调控决策，统计部门对外来人口和当地人口进行了买房的心理预期调研，用简单随机抽样的方法抽取了110人进行统计，得到如下列联表（不全）：

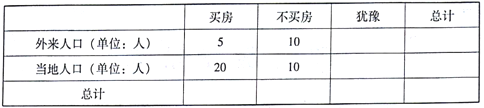
    已知样本中外来人口数与当地人口数之比为3:8.

    （1）补全上述列联表；

    （2）从参与调研的外来人口中用分层抽样方法抽取6人，进一步统计外来人口的某项收入指标，若一个买房人的指标记为3，一个犹豫人的指标记为2，一个不买房人的指标记为1，现在从这6人中再随机选取3人，用表示这3人指标之和，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣（a+1）x+1（a∈R）
    （1）若关于x的不等式f（x）＞0的解集为R，求实数a的取值范围；
    （2）若关于x的不等式f（x）≤0的解集为P，集合Q={x|0≤x≤1}，若P∩Q=，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥P﹣ABCD的底面ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，PA= ．
    （Ⅰ）证明：平面PBE⊥平面PAB；
    （Ⅱ）求二面角A﹣BE﹣P的大小．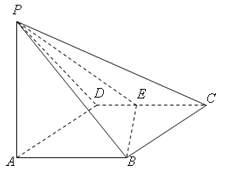

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知两点A（﹣1，2），B（m，3）．且实数m∈[﹣ ﹣1， ﹣1]，求直线AB的倾斜角α的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，已知AB⊥侧面BB1C1C，CB⊥C1B，BC=1，CC1=2，A1B1= ，
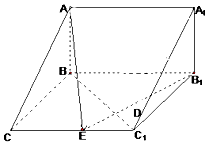
    （1）试在棱CC1（不包含端点C，C1）上确定一点E的位置，使得EA⊥EB1；
    （2）在（1）的条件下，求AE和BC1所成角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）=lg（ax﹣1）﹣lg（x﹣1）在区间[2，+∞）上是增函数，则a的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知，在直角坐标系中，直线的参数方程为（为参数）；在以坐标原点为极点， 轴的正半轴为极轴的极坐标系中，直线的极坐标方程是.

    （Ⅰ）求证： ；

    （Ⅱ）设点的极坐标为， 为直线， 的交点，求的最大值.

    查看答案和解析>>

    同步练习册答案