(本小题满分12分)已知函数
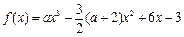
.
(1)当
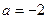
时,求函数
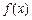
的单调区间和极值;
(2)当
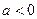
时,试求方程
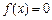
根的个数.
(1)

的单调递减区

间为

和
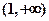
,单调递增区间为(-1,1)


(2)当
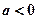
时,

有三个零点

.

(1)当
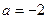
时,

令

得


∴

的单调递减区

间为

和
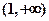
,单调递增区间为(-1,1)


(6分)
(2) 当
a<0时,

 f
f(
x)在

,
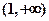
递减;在

递增, (9分)
又

,

(11分)
 f
f(
x)有三个零点.


当
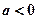
时,

有三个零点

. (12分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本题15分)已知函数
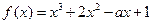
.
(I)若函数
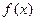
在点
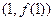
处的切线斜率为4,求实数
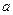
的值;
(II)若函数
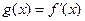
在区间
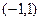
上存在零点,求实数
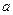
的取值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)
已知函数
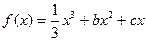
(b、c为常数)的两个极值点分别为
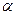
、
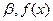
在点
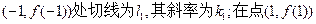
处的切线为
l2,其斜率为k
2。
(1)若
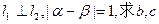
;
(2)若
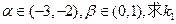
的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
函数f(x)=e

lnx的导数是_____
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
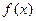
是R上的可导函数,且
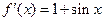
,则函数
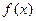
的解析式可以为
.
(只须写出一个符合题意的函数解析式即可);
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
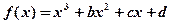
(
b,c,d为常数),当
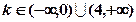
时,
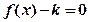
只有一个实数根;当
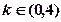
时,
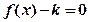
有3个相异实根,现给出下列4个命题:
①函数
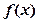
有2个极值点; ②
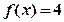
和
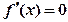
有一个相同的实根;
③函数
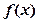
有3个极值点; ④
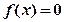
和
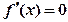
有一个相同的实根,其中是真命题的是
(填真命题的序号)。
查看答案和解析>>

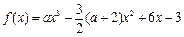 .
.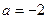 时,求函数
时,求函数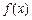 的单调区间和极值;
的单调区间和极值; 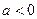 时,试求方程
时,试求方程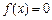 根的个数.
根的个数. 走进文言文系列答案
走进文言文系列答案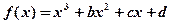 (b,c,d为常数),当
(b,c,d为常数),当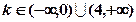 时,
时,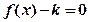 只有一个实数根;当
只有一个实数根;当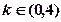 时,
时,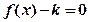 有3个相异实根,现给出下列4个命题:
有3个相异实根,现给出下列4个命题: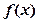 有2个极值点; ②
有2个极值点; ②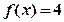 和
和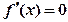 有一个相同的实根;
有一个相同的实根;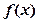 有3个极值点; ④
有3个极值点; ④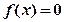 和
和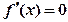 有一个相同的实根,其中是真命题的是 (填真命题的序号)。
有一个相同的实根,其中是真命题的是 (填真命题的序号)。