
分析 (1)根据$\overrightarrow{m}$•$\overrightarrow{n}$=2acosB,得a=2acosB,求出B的值即可;(2)根据三角形的面积求出ac=8,由a+c=6,联立方程组,求出a,c的值,根据余弦定理求出b的值即可.
解答 解:(1)由$\overrightarrow{m}$=(a,0),$\overrightarrow{n}$=(1,cosB),
$\overrightarrow{m}$•$\overrightarrow{n}$=2acosB,得a=2acosB,
故cosB=$\frac{1}{2}$,得B=$\frac{π}{3}$;
(2)S△ABC=$\frac{1}{2}$acsinB=2$\sqrt{3}$得ac=8,
联立$\left\{\begin{array}{l}{ac=8}\\{a+c=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=4}\\{c=2}\end{array}\right.$或$\left\{\begin{array}{l}{a=2}\\{c=4}\end{array}\right.$,
由余弦定理得b2=16+4-8=12,
解得:b=2$\sqrt{3}$.
点评 本题考查了向量的乘法,考查余弦定理的应用,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $(\frac{7π}{12},0)$是函数y=f(x)的对称中心 | B. | $x=\frac{7π}{12}$是函数y=f(x)的对称轴 | ||
| C. | $(-\frac{π}{12},0)$是函数y=f(x)的对称中心 | D. | $x=-\frac{π}{12}$是函数y=f(x)的对称轴 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.
如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (2,3) | C. | $[{\frac{7}{3},3})$ | D. | $({1,\frac{7}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图正四面体(所有棱长都相等)D-ABC中,动点P在平面BCD上,且满足∠PAD=30°,若点P在平面ABC上的射影为P′,则sin∠P′AB的最大值为( )
如图正四面体(所有棱长都相等)D-ABC中,动点P在平面BCD上,且满足∠PAD=30°,若点P在平面ABC上的射影为P′,则sin∠P′AB的最大值为( )| A. | $\frac{2\sqrt{7}}{7}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
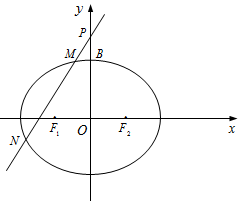 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,0] | C. | (-$\frac{1}{2}$,+∞) | D. | (0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com