Question

15．如图是某圆拱桥的示意图，这个圆拱桥的水面跨度AB=24m，拱高OP=8m．问：为使宽为10m的船能从桥下顺利通过，应如何限制船体及装载的货物在水面以上的高度？

Answer 1

分析 假设$\widehat{AB}$所在圆的圆心为点O′，连接O′A，O′M，O′O，先由垂径定理求出AO的长，设O′A=r，则OO′=r-OP，利用勾股定理求出r的值，进而可得出OO′的长，在Rt△MO′E中假设ME=5，利用勾股定理求出OE的长即可．

解答 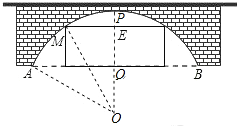解：假设$\widehat{AB}$所在圆的圆心为点O′，连接O′A，O′M，O′O，
∵AB=24m，OP=8m，AB⊥OP，
∴AO=OB=$\frac{1}{2}$AB=12m．
设O′A=r，则OO′=r-OP，
在Rt△AOO′中，r²=（r-8）²+12²，解得r=13m，
∴OO′=13-8=5m，
在Rt△MO′E中，假设ME=5m，
则13²=OE²+5²，解得OE=12m，
∴OE=O′E-OO′=12-5=7m，
∴为使宽为10m的船能从桥下顺利通过，限制船体及装载的货物在水面以上的高度小于等于7m．

点评 本题考查圆的方程，考查学生的计算能力，正确求出圆的半径是关键．