
 、
、 、
、 两两所成的角相等,并且|
两两所成的角相等,并且| |=1,|
|=1,| |=2,|
|=2,| |=3.
|=3. +
+ +
+ 的长度;
的长度; +
+ +
+ 与
与 的夹角.
的夹角. +
+ +
+ |=
|=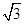 .(Ⅱ)
.(Ⅱ) 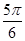 .
. 、
、 、
、 两两所成的角均为
两两所成的角均为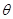 ,则
,则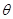 =0或
=0或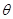 =
=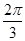 , 又|
, 又| |=1,|
|=1,| |=2,|
|=2,| |=3.则当
|=3.则当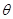 =0时,
=0时, ·
· =|
=| |·|
|·| |
|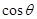 =2,
=2, ·
· =|
=| |·|
|·| |
|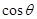 =6,
=6, ·
· =|
=| |·|
|·| |
|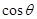 =3,此时 |
=3,此时 | +
+ +
+ |2=
|2= 2+
2+ 2+
2+ 2+2
2+2 ·
· +2
+2 ·
· +2
+2 ·
· =14+22=36,∴ |
=14+22=36,∴ | +
+ +
+ |=6;
|=6;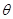 =
=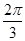 时,
时, ·
· =|
=| |·|
|·| |
|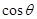 =-1,
=-1, ·
· =|
=| |·|
|·| |
|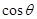 =-3,
=-3, ·
· =|
=| |·|
|·| |
|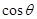 =-
=-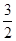 ,此时 |
,此时 | +
+ +
+ |2=
|2= 2+
2+ 2+
2+ 2+2
2+2 ·
· +2
+2 ·
· +2
+2 ·
· =14-11=3,∴ |
=14-11=3,∴ | +
+ +
+ |=
|=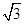 .
.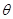 =0,即|
=0,即| +
+ +
+ |=6时,
|=6时, +
+ +
+ 与
与 的夹角显然为0; 当
的夹角显然为0; 当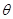 =
=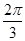 ,即|
,即| +
+ +
+ |=
|=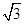 时,∵ (
时,∵ ( +
+ +
+ )·
)· =-
=-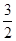 ,且|
,且| +
+ +
+ |·|
|·| |=
|=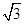 ,
,  <
< +
+ +
+ ,
, >=-
>=-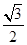 ,∴
,∴ +
+ +
+ 与
与 的夹角为
的夹角为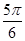 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:填空题
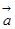 //
//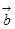 ,
,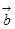 //
//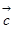 ,则
,则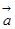 //
//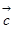
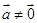 ,
,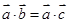 ,则
,则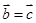 ;
;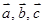 都有
都有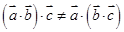 ;
;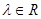 使得
使得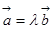 ,则向量
,则向量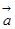 //
//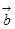 ;
;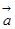 //
//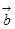 ,则存在
,则存在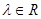 使得
使得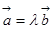 ;
;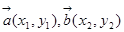 ,若
,若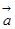 //
//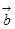 ,则
,则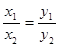 其中正确的是
其中正确的是 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com