
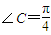 ,求∠A的大小.
,求∠A的大小.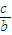 的取值范围.
的取值范围.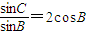 ,可得sinC=2sinBcosB=sin2B,由此可得C=2B或C+2B=π,最后结合三角形内角和定理和
,可得sinC=2sinBcosB=sin2B,由此可得C=2B或C+2B=π,最后结合三角形内角和定理和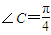 ,即可算出∠A的大小.
,即可算出∠A的大小.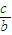 化简整理得
化简整理得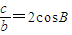 .利用△ABC是锐角三角形,得到B∈(
.利用△ABC是锐角三角形,得到B∈(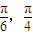 ),结合余弦函数的图象与性质,即可得出
),结合余弦函数的图象与性质,即可得出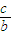 的取值范围.
的取值范围.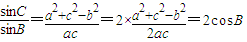 …(2分)
…(2分)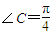 ,可得
,可得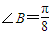 ,所以
,所以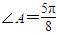 …(5分)
…(5分)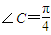 ,则
,则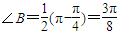 ,可得
,可得 …(6分)
…(6分)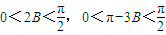
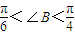 …(10分)
…(10分)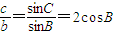 …(12分)
…(12分)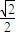 ,
,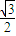 ),∴可得
),∴可得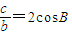 =
=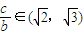 …(14分)
…(14分)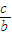 的取值范围.着重考查了利用正余弦定理解三角形、三角形内角和定理与余弦函数的图象与性质等知识,属于中档题.
的取值范围.着重考查了利用正余弦定理解三角形、三角形内角和定理与余弦函数的图象与性质等知识,属于中档题. 

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| c |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| x0 |
| 2 |
| ||
| 3 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 12 |
| A |
| 2 |
| π |
| 8 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| 3 |
| m |
| n |
| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| π |
| 4 |
| n |
| π |
| 4 |
| 3 |
| m |
| n |
| 3 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com