
分析 通过展开式中第五项的系数与第三项的系数的比是10:1得到n值,然后求要求的特征项.
解答 解:(1)由题意,第五项系数和第三项系数比值是10,即$\frac{{C}_{n}^{4}•(-2)^{4}}{{C}_{n}^{2}•(-2)^{2}}$=10,
化简得n2-5n-24=0,解得n=8或n=-3(舍去).
(1)令x=1得各项系数和为(1-2)8=1;二项式系数和28=256;
(2)通项公式为Tr+1=$(-2)^{r}{C}_{8}^{r}{x}^{4-\frac{5r}{2}}$,
令4-$\frac{5r}{2}$=-1,则r=2,
所以展开式中含x-1的项的系数为112;
(3)由2r-1C8r-1≥2rC8r,2r-1C8r-1≥2r-2C8r-2,解得r=5或6,
∴展开式中系数绝对值最大的项为T6=-1792${x}^{-\frac{17}{2}}$,T7=1792x11.
点评 本题考查了二项式定理的运用;关键是利用已知求出指数后,找出二项式的展开式通项,根据x的指数求特征项.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一或第二象限的角都可作为三角形的内角 | |
| B. | 钝角比第三象限的角小 | |
| C. | 第四象限的角一定是负角 | |
| D. | 始边相同而终边不同的角一定不相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 销售单价/万元 | [8,10) | [10,12) | [12,14) | [14,16) | [16,18) | [18,20] |
| 频数/辆 | 5 | 10 | 20 | a | 20 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
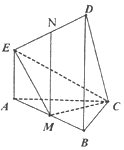 如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.
如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 2.5 | 3 | 4 | 4.5 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com