
定义函数 为
为 的
的 阶函数.
阶函数.
(1)求一阶函数 的单调区间;
的单调区间;
(2)讨论方程 的解的个数;
的解的个数;
(3)求证: .
.
(1)当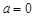 时,
时,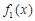 无单调区间;
无单调区间;
当 时,
时,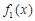 的单增区间为
的单增区间为 单减区间为
单减区间为 ;
;
当 时,
时,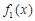 的单增区间为
的单增区间为 ,单减区间为
,单减区间为 ;
;
(2)当 时,方程有两个不同解.当
时,方程有两个不同解.当 时,方程有0个解.当
时,方程有0个解.当 或
或 时,方程有唯一;
时,方程有唯一;
(3)详见解析.
解析试题分析:(1)求导,对 分情况讨论;
分情况讨论;
(2)研究方程的解的个数,实质就是研究函数的图象.通过求导,弄清函数的单调区间及函数值的范围,结合图象即可知道方程 的解的个数.
的解的个数.
(3)将所要证明的不等式与题中函数联系起来看,应该考查 的3阶函数,且令
的3阶函数,且令 ,即
,即 .将这个函数求导得
.将这个函数求导得 .由
.由 得
得
则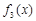 在
在 单调递增,在
单调递增,在 单调递减. 这样可得
单调递减. 这样可得 的最大值,从而得到所要证明的不等式.
的最大值,从而得到所要证明的不等式.
试题解析:(1) ,
,
令 ,当
,当 时,
时,
 当
当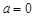 时,
时,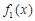 无单调区间;
无单调区间;
当 时,
时,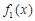 的单增区间为
的单增区间为 单减区间为
单减区间为 .
.
当 时,
时,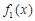 的单增区间为
的单增区间为 ,单减区间为
,单减区间为 . 4分.
. 4分.
(2)由 当
当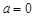 时,方程无解.当
时,方程无解.当 时,
时,
令 则
则 由
由 得
得
从而 在
在 单调递增,在
单调递增,在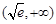 单调递减.
单调递减.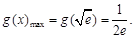
当 时,
时, ,当
,当

 当
当 ,即
,即 时,方程有两个不同解.
时,方程有两个不同解.
当 ,即
,即 时,方程有0个解
时,方程有0个解
当 ,
, 或即
或即 或
或 时,方程有唯一解.
时,方程有唯一解.
综上,当 时,方程有两个不同解.当
时,方程有两个不同解.当 时,方程有0个解.当
时,方程有0个解.当 或
或 时,方程有唯一解.
时,方程有唯一解.  9分.
9分.
(3)特别地,当 时
时
由 得
得 .
.
由 得
得
则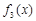 在
在 单调递增,在
单调递增,在 单调递减.
单调递减.

 即
即 .又
.又 时,
时,
 &
&


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某市在市内主干道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为O,半径为100m,并与北京路一边所在直线 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位:
的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位: ),
), (单位:弧度).
(单位:弧度).
(I)将S表示为 的函数;
的函数;
(II)当绿化面积S最大时,试确定点A的位置,并求最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施不能建设开发,且要求用栏栅隔开(栏栅要求在直线上),公共设施边界为曲线 的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设
的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设 .
.
(I)将 (O为坐标原点)的面积S表示成f的函数S(t);
(O为坐标原点)的面积S表示成f的函数S(t);
(II)若 ,S(t)取得最小值,求此时a的值及S(t)的最小值.
,S(t)取得最小值,求此时a的值及S(t)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com