分析:(Ⅰ)由已知,p在平面ABC内的射影是Rt△ABC的外心,即斜边BC的中点O.取AC的中点D,连PD,DO,PO,根据三垂线定理,∠PDO 为所求,再解三角形求出二面角的大小即可.
(Ⅱ)利用等体积变换,V
P-ABC=V
B-PAC=
S△APC•h,其中点B到平面PAC的距离,求出三角形PAC的面积,代入求解即可.
解答:解:
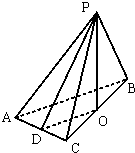
(Ⅰ)∵侧棱PA、PB、PC与底面ABC所成的角相等,
∴点P在平面ABC内的射影是Rt△ABC的外心,即斜边BC的中点O
取AC的中点D,连PD,DO,PO,则
VP-ABC=(•AC•AB)•OP=(•4•4)•OP=16,
∴OP=6.∵OP⊥平面ABC,
∴OD是PD在平面ABC内的射影,
∵AC⊥OD,∴AC⊥PD.∴∠PDO为二面角P-AC-B的平面角.
在Rt△POD中,
tan∠PDO==,
∴
∠PDO=,
故二面角P-AC-B的大小为
.
(Ⅱ)∵AC=4,
PD==4,
∴
S△APC=AC•PD=8.
设点B到平面PAC的距离为h,则由V
P-ABC=
S△APC•h=16解方程得h=6,∴点B到平面PAC的距离等于6.
点评:本题考查二面角、点到平面距离的计算,考查学生空间想象能力,计算能力、转化能力.空间问题平面化,是解决空间问题最核心的思想方法. 在点到平面距离的计算问题中,利用等体积变换也是常用方法,好处在于不用具体作出点到面的垂线段.

 在三棱锥P-ABC中,AB⊥AC,AC=4,AB=4
在三棱锥P-ABC中,AB⊥AC,AC=4,AB=4 (Ⅰ)∵侧棱PA、PB、PC与底面ABC所成的角相等,
(Ⅰ)∵侧棱PA、PB、PC与底面ABC所成的角相等,

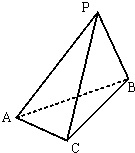
 在三棱锥P-ABC中,PA⊥平面ABC.
在三棱锥P-ABC中,PA⊥平面ABC. (2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
(2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.