
【题目】设![]() 为正整数,各项均为正整数的数列
为正整数,各项均为正整数的数列![]() 定义如下:
定义如下: ![]() ,
,
(1)若![]() ,写出
,写出![]() ,
,![]() ,
,![]() ;
;
(2)求证:数列![]() 单调递增的充要条件是
单调递增的充要条件是![]() 为偶数;
为偶数;
(3)若![]() 为奇数,是否存在
为奇数,是否存在![]() 满足
满足![]() ?请说明理由.
?请说明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)证明见解析;(3)存在,理由见解析.
;(2)证明见解析;(3)存在,理由见解析.
【解析】
(1)![]() 时,结合条件,注意求得
时,结合条件,注意求得![]() ,
,![]() ,
,![]() ;
;
(2)根据![]() 与零的关系,判断数列
与零的关系,判断数列![]() 单调递增的充要条件;
单调递增的充要条件;
(3)存在![]() 满足
满足![]() .
.
(1)![]() ,
,![]() ,
,![]() .
.
(2)先证“充分性”.
当![]() 为偶数时,若
为偶数时,若![]() 为奇数,则
为奇数,则![]() 为奇数.
为奇数.
因为![]() 为奇数,所以归纳可得,对
为奇数,所以归纳可得,对![]() ,
,![]() 均为奇数,则
均为奇数,则![]() ,
,
所以![]() ,
,
所以数列![]() 单调递增.
单调递增.
再证“必要性”.
假设存在![]() 使得
使得![]() 为偶数,则
为偶数,则![]() ,与数列
,与数列![]() 单调递增矛盾,
单调递增矛盾,
因此数列![]() 中的所有项都是奇数.
中的所有项都是奇数.
此时![]() ,即
,即![]() ,所以
,所以![]() 为偶数.
为偶数.
(3)存在![]() 满足
满足![]() ,理由如下:
,理由如下:
因为![]() ,
,![]() 为奇数,所以
为奇数,所以![]() 且
且![]() 为偶数,
为偶数,![]() .
.
假设![]() 为奇数时,
为奇数时, ![]() ;
;![]() 为偶数时,
为偶数时,![]() .
.
当![]() 为奇数时,
为奇数时,![]() ,且
,且![]() 为偶数;
为偶数;
当![]() 为偶数时,
为偶数时,![]() .
.
所以若![]() 为奇数,则
为奇数,则![]() ;若
;若![]() 为偶数,则
为偶数,则![]() .
.
因此对![]() 都有
都有![]() .
.
所以正整数数列![]() 中的项的不同取值只有有限个,所以其中必有相等的项.
中的项的不同取值只有有限个,所以其中必有相等的项.
设集合![]() ,设集合
,设集合![]() .
.
因为![]() ,所以
,所以![]() .
.
令![]() 是
是![]() 中的最小元素,下面证
中的最小元素,下面证![]() .
.
设![]() 且
且![]() .
.
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() .
.
所以若![]() ,则
,则![]() 且
且![]() ,与
,与![]() 是
是![]() 中的最小元素矛盾.
中的最小元素矛盾.
所以![]() ,且存在
,且存在![]() 满足
满足![]() ,即存在
,即存在![]() 满足
满足![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展,下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
参考公式: ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()

(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2py(p>0),直线l交C于A,B两点,且A,B两点与原点不重合,点M(1,2)为线段AB的中点.
(1)若直线l的斜率为1,求抛物线C的方程;
(2)分别过A,B两点作抛物线C的切线,若两条切线交于点S,证明点S在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() 相邻对称轴之间的距离为
相邻对称轴之间的距离为![]() ,且函数
,且函数![]() 在
在![]() 处取得最大值,则下列命题正确的个数为( )
处取得最大值,则下列命题正确的个数为( )
①当![]() 时,m的取值范围是
时,m的取值范围是 ;②将
;②将![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数为偶函数;③函数
个单位后所对应的函数为偶函数;③函数![]() 的最小正周期为
的最小正周期为![]() ;④函数
;④函数![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为定义在
为定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,有
时,有![]() ,且当
,且当![]() 时,
时,![]() ,下列命题正确的是( )
,下列命题正确的是( )
A.![]() B.函数
B.函数![]() 在定义域上是周期为
在定义域上是周期为![]() 的函数
的函数
C.直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点D.函数
个交点D.函数![]() 的值域为
的值域为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了节能减排,发展低碳经济,我国政府从2001年起就通过相关政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
中国新能源汽车产销情况一览表 | ||||
新能源汽车生产情况 | 新能源汽车销售情况 | |||
产品(万辆) | 比上年同期 | 销量(万辆) | 比上年同期 | |
2018年3月 | 6.8 | 105 | 6.8 | 117.4 |
4月 | 8.1 | 117.7 | 8.2 | 138.4 |
5月 | 9.6 | 85.6 | 10.2 | 125.6 |
6月 | 8.6 | 31.7 | 8.4 | 42.9 |
7月 | 9 | 53.6 | 8.4 | 47.7 |
8月 | 9.9 | 39 | 10.1 | 49.5 |
9月 | 12.7 | 64.4 | 12.1 | 54.8 |
10月 | 14.6 | 58.1 | 13.8 | 51 |
11月 | 17.3 | 36.9 | 16.9 | 37.6 |
1-12月 | 127 | 59.9 | 125.6 | 61.7 |
2019年1月 | 9.1 | 113 | 9.6 | 138 |
2月 | 5.9 | 50.9 | 5.3 | 53.6 |

根据上述图表信息,下列结论错误的是( )
A.2017年3月份我国新能源汽车的产量不超过![]() 万辆
万辆
B.2017年我国新能源汽车总销量超过![]() 万辆
万辆
C.2018年8月份我国新能源汽车的销量高于产量
D.2019年1月份我国插电式混合动力汽车的销量低于![]() 万辆
万辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为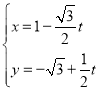 (t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系.曲线C的极坐标方程为
(t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系.曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)设点![]() ,直线l与曲线C相交于A,B两点,求
,直线l与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,已知
中,已知![]() ,
,![]() 对任意
对任意![]() 都成立,数列
都成立,数列![]() 的前n项和为
的前n项和为![]() .
.
(1)若![]() 是等差数列,求k的值;
是等差数列,求k的值;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)是否存在实数k,使数列![]() 是公比不为1的等比数列,且任意相邻三项
是公比不为1的等比数列,且任意相邻三项![]() ,
,![]() ,
,![]() 按某顺序排列后成等差数列?若存在,求出所有k的值;若不存在,请说明理由.
按某顺序排列后成等差数列?若存在,求出所有k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com