
【题目】已知向量![]() ,
,![]() ,
,![]() ,
,![]() ,函数
,函数![]() ,
,![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求![]() 的单调增区间;
的单调增区间;
(2)方程![]() ;在
;在![]() 上有且只有一个解,求实数n的取值范围;
上有且只有一个解,求实数n的取值范围;
(3)是否存在实数m满足对任意x1∈[-1,1],都存在x2∈R,使得![]() +
+![]() +m(
+m(![]() -
-![]() )+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由.
)+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由.
【答案】(1)![]() ,
,![]() (2)
(2)![]() 或
或![]() (3)存在,且m取值范围为
(3)存在,且m取值范围为![]()
【解析】
(1)函数![]() ,
,![]() 的最小正周期为
的最小正周期为![]() .可得
.可得![]() ,即可求解
,即可求解![]() 的单调增区间.
的单调增区间.
(2)根据x在![]() 上求解
上求解![]() 的值域,即可求解实数n的取值范围;
的值域,即可求解实数n的取值范围;
(3)由题意,求解![]() 的最小值,利用换元法求解
的最小值,利用换元法求解![]() 的最小值,即可求解m的范围.
的最小值,即可求解m的范围.
(1)函数f(x)![]()
![]() 1=2sin2(ωx
1=2sin2(ωx![]() )
)![]() cos(2ωx)﹣1
cos(2ωx)﹣1
=sin(2ωx)![]() cos(2ωx)
cos(2ωx)
=2sin(2ωx![]() )
)
∵f(x)的最小正周期为π.ω>0
∴![]() ,
,
∴ω=1.
那么f(x)的解析式f(x)=2sin(2x![]() )
)
令![]() 2x
2x![]() ,k∈Z
,k∈Z
得:![]() x
x![]()
∴f(x)的单调增区间为[![]() ,
,![]() ],k∈Z.
],k∈Z.
(2)方程f(x)﹣2n+1=0;在[0,![]() ]上有且只有一个解,
]上有且只有一个解,
转化为函数y=f(x)+1与函数y=2n只有一个交点.
∵x在[0,![]() ]上,
]上,
∴![]() (2x
(2x![]() )
)![]()
那么函数y=f(x)+1=2sin(2x![]() )+1的值域为[
)+1的值域为[![]() ,2],结合图象可知
,2],结合图象可知
函数y=f(x)+1与函数y=2n只有一个交点.
那么![]() 2n<1或2n=2,
2n<1或2n=2,
可得![]() 或n=1.
或n=1.
(3)由(1)可知f(x)=2sin(2x![]() )
)
∴f(x2)min=﹣2.
实数m满足对任意x1∈[﹣1,1],都存在x2∈R,
使得![]() m(
m(![]() )+1>f(x2)成立.
)+1>f(x2)成立.
即![]() m(
m(![]() )+1>﹣2成立
)+1>﹣2成立
令y![]() m(
m(![]() )+1
)+1
设![]() t,那么
t,那么![]() (
(![]() )2+2=t2+2
)2+2=t2+2
∵x1∈[﹣1,1],
∴t∈[![]() ,
,![]() ],
],
可得t2+mt+5>0在t∈[![]() ,
,![]() ]上成立.
]上成立.
令g(t)=t2+mt+5>0,
其对称轴t![]()
∵t∈[![]() ,
,![]() ]上,
]上,
∴①当![]() 时,即m≥3时,g(t)min=g(
时,即m≥3时,g(t)min=g(![]() )
)![]() ,解得
,解得![]() ;
;
②当![]() ,即﹣3<m<3时,g(t)min=g(
,即﹣3<m<3时,g(t)min=g(![]() )
)![]() 0,解得﹣3<m<3;
0,解得﹣3<m<3;
③当![]() ,即m≤﹣3时,g(t)min=g(
,即m≤﹣3时,g(t)min=g(![]() )
)![]() 0,解得
0,解得![]() m≤﹣3;
m≤﹣3;
综上可得,存在m,可知m的取值范围是(![]() ,
,![]() ).
).


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】下列四个命题:
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型拟合的效果越好;
越小,说明模型拟合的效果越好;
③散点图中所有点都在回归直线附近;
④随机误差![]() 满足
满足![]() ,其方差
,其方差![]() 的大小可用来衡量预报精确度.
的大小可用来衡量预报精确度.
其中正确命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一网购狂欢节”源于淘宝商城(天猫)2009年11月11 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是11月11日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)根据(1)的判断结果,建立![]() 与
与![]() 之间的回归方程,并预测当
之间的回归方程,并预测当![]() 时,对应的利润
时,对应的利润![]() 为多少(
为多少(![]() 精确到0.1).
精确到0.1).
附参考公式:回归方程中![]() 中
中![]() 和
和![]() 最小二乘估计分别为
最小二乘估计分别为
 ,相关系数
,相关系数
参考数据:
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行抽奖活动,从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于6中特等奖,等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中二等奖的概率;
(2)求未中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)将![]() ,
, ![]() 的方程化为普通方程,并说明它们分别表示什么曲线?
的方程化为普通方程,并说明它们分别表示什么曲线?
(2)以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .若
.若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 为
为![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
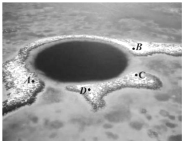
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某营养协会对全市18岁男生的身高作调查,统计显示全市18岁男生的身高服从正态分布![]() ,现某校随机抽取了100名18岁男生的身高分析,结果这100名学生的身高全部介于
,现某校随机抽取了100名18岁男生的身高分析,结果这100名学生的身高全部介于![]() 到
到![]() 之间.现将结果按如下方式分为6组,第一组
之间.现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
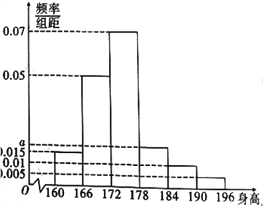
(1)若全市18岁男生共有![]() 人,试估计该市身高在
人,试估计该市身高在![]() 以上的18岁男生人数;
以上的18岁男生人数;
(2)求![]() 的值,并计算该校18岁男生的身高的中位数(精确到小数点后三位);
的值,并计算该校18岁男生的身高的中位数(精确到小数点后三位);
(3)若身高![]() 以上的学生校服需要单独定制,现从这100名学生中身高在
以上的学生校服需要单独定制,现从这100名学生中身高在![]() 以上的同学中任意抽取3人,这三人中校服需要单独定制的人数记为
以上的同学中任意抽取3人,这三人中校服需要单独定制的人数记为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附: ![]() ,则
,则![]() ;
;
![]() ,则
,则![]() ;
;
![]() ,则
,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com