
����Ŀ�����г����飬ij��Ʒÿ�ֵļ۸�Ϊx��1��x��14����Ԫʱ������Ʒ���¹�����Ϊy1�֣�y1=ax+ ![]() a2��a��a��0������������Ϊy2�֣�y2=��
a2��a��a��0������������Ϊy2�֣�y2=�� ![]() x2��
x2�� ![]() x+1��������Ʒ�����������ڹ�����ʱ�����������ڹ�������������Ʒ�������������ڹ�����ʱ������������������������Ʒ�������۶��������������۸�ij˻���
x+1��������Ʒ�����������ڹ�����ʱ�����������ڹ�������������Ʒ�������������ڹ�����ʱ������������������������Ʒ�������۶��������������۸�ij˻���
��1����֪a= ![]() ����ij�¸���Ʒ�ļ۸�Ϊx=7������Ʒ�ڸ��µ����۶��ȷ��1Ԫ����
����ij�¸���Ʒ�ļ۸�Ϊx=7������Ʒ�ڸ��µ����۶��ȷ��1Ԫ����
��2�����������빩�������ʱ�ļ۸�Ϊ����۸�������Ʒ�ľ���۸���ÿ��6��Ԫ����ʵ��a��ȡֵ��Χ��
���𰸡�
��1���⣺��a= ![]() ��x=7ʱ��y1=
��x=7ʱ��y1= ![]() ��7+
��7+ ![]() ����
���� ![]() ��2��
��2�� ![]() =1+
=1+ ![]() ��
�� ![]() =
= ![]() ��
��
y2=�� ![]() ����
���� ![]() ��2��
��2�� ![]() ��
�� ![]() +1=
+1= ![]() ��
��
��y1��y2��
��������۶�Ϊ7�� ![]() ��104��50313��Ԫ��
��104��50313��Ԫ��
��2���⣺��f��x��=y1��y2= ![]() x2+��
x2+�� ![]() +a��x��a��1��
+a��x��a��1��
��f��x����[6��14��������㣬
��a��0����f��0��=��a��1��0����f��x����ͼ�����ϣ�
��f��x����[6��14����ֻ��1����㣬
�� ![]() ����
���� 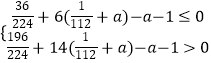 ��
��
��ã�0��a�� ![]()
����������1������y1 �� y2 �� �Ƚϴ�Сȷ�����������ټ������۶��2����f��x��=y1��y2 �� ��f��x����[6��14��������㣬�������Ĵ����Զ����в���ʽ����a�ķ�Χ��


 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ��Ŵ���������ѧר������������������һ�������������������������������룬��ȥ����һǧһ�ٶ�ʮ�������������һ�����������һʮ������������о�ʮ����ռ�������������룬����ӭ������������꣮�ʣ�������ꣿ�� ��
A.8��
B.9��
C.12��
D.16��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x0��Rʹ�ù���x�IJ���ʽ|x��1|��|x��2|��t������
��1��������������ʵ��t����T��
��2����m��1��n��1���Ҷ���t��T������ʽlog3mlog3n��t�����������m+n����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
�� ![]() ������
������ ![]() ����
���� ![]() �ϵĵ����������෴���ش��������⣺
�ϵĵ����������෴���ش��������⣺
��1������ ![]() ��
�� ![]() ������ʽ
������ʽ ![]() ���������ʵ��
���������ʵ�� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���� ![]() ������ʵ��
������ʵ�� ![]() ��
�� ![]() ����
���� ![]() ����֤��
����֤�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4��5������ʽѡ��
��֪ ![]() =
= ![]() ��
�� ![]() ����
����
���� ![]() ʱ���ⲻ��ʽ
ʱ���ⲻ��ʽ ![]() ��
��
����������ʽ ![]() ��
�� ![]() ���������ʵ��
���������ʵ�� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}����a1=12��a1+2a2+3a3+��+nan=n2an �� ��a2017= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}��ǰn��a1 �� a2 �� ����an��n��N*����ɼ���An={a1 �� a2 �� ����an}���Ӽ���An����ȡk��k=1��2��3������n�������������п��ܵ�k�����ij˻��ĺ�ΪTk����ֻȡһ�������涨�˻�Ϊ���������������磺��������{2n��1}����n=1ʱ��A1={1}��T1=1��n=2ʱ��A2={1��3}��T1=1+3��T2=13��
��1��������An={1��3��5������2n��1}����n=3ʱ��T1 �� T2 �� T3��ֵ��
��2��������An={1��3��7������2n��1}��֤����n=kʱ����Ak��Tm��n=k+1ʱ����Ak+1��Tm��Ϊ����ʾ������Tm���ʾ���й�ϵʽTm��=��2k+1��1��Tm��1+Tm �� ����m��k��N*��2��m��k��
��3�����ڣ�2���м���An �� ����Sn=T1+T2+��+Tn �� ��Sn����n��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() =��1��0����
=��1��0���� ![]() =��1��1������x��y��=
=��1��1������x��y��= ![]() ����0�ܦˡ�1�ܦ̡�2ʱ��z=
����0�ܦˡ�1�ܦ̡�2ʱ��z= ![]() ��m��0��n��0�������ֵΪ2����m+n����СֵΪ
��m��0��n��0�������ֵΪ2����m+n����СֵΪ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}�Ǽ���{x|x=3s+3t �� s��t��s��t��N}�����е�����С�������гɵ����У���a1=4��a2=10��a3=12��a4=28��a5=30��a6=36������������{an}�и������С�´���С�Ҵ��ԭ���ų���ͼ�ĵ���ֱ����������������a15��ֵΪ �� 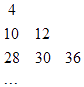
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com