
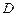 的函数
的函数 ,若有常数M,使得对任意的
,若有常数M,使得对任意的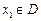 ,存在唯一的
,存在唯一的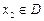 满足等式
满足等式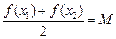 ,则称M为函数
,则称M为函数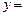 f (x)的“均值”.
f (x)的“均值”.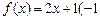 ≤
≤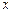 ≤
≤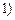 的“均值”,请说明理由;
的“均值”,请说明理由;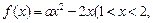
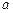 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围; 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).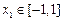 ,有
,有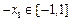 ,
,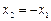 时,有
时,有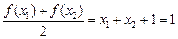 ,
, 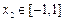 ,满足
,满足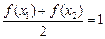
 , ……………………2分
, ……………………2分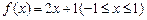 的“均值”. ……………………4分
的“均值”. ……………………4分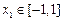 ,有
,有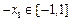 ,令
,令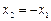 ,
,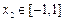 ,且
,且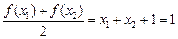 ,
, 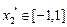 ,且
,且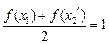 ,则有
,则有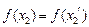 ,可得
,可得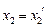 ,
,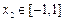 ,满足
,满足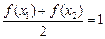 , ……………………2分
, ……………………2分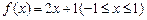 的“
的“ 均值”. ……………………4分)
均值”. ……………………4分)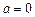 时,
时,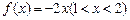 存在“均值”,且“均值”为
存在“均值”,且“均值”为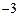 ;…………5分
;…………5分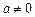 时,由
时,由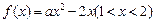 存在均值,可知对任意的
存在均值,可知对任意的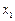 ,
,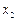 与之对应,从而有
与之对应,从而有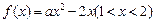 单调,
单调,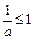 或
或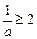 ,解得
,解得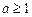 或
或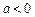 或
或 , ……………………9分
, ……………………9分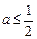 或
或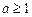 . ……………………10分
. ……………………10分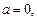
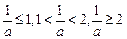 四种情形
四种情形 进行讨论)
进行讨论)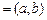 或
或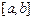 时,函数
时,函数 存在唯一的“均值”.
存在唯一的“均值”. 的“均值”为
的“均值”为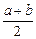 ; …………………12分
; …………………12分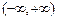 时,函数
时,函数 存在无数多个“均值”.
存在无数多个“均值”. 的“均值”; ……………………14分
的“均值”; ……………………14分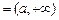 或
或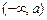 或
或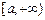 或
或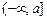 或
或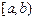 或
或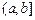 时,
时, 不存在“均值”. ……………………16分
不存在“均值”. ……………………16分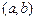 、
、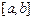 其中之一时,函数
其中之一时,函数 存在唯一的“均值”.
存在唯一的“均值”. 的“均值”为
的“均值”为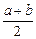 ; ……………………13分
; ……………………13分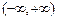 时,函数
时,函数 存在无数多个“均值”.
存在无数多个“均值”. 的“均值”; ……………………16分
的“均值”; ……………………16分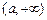 、
、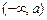 、
、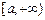 、
、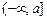 、
、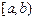 、
、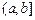 其中之一时,函数
其中之一时,函数 不存在“均值”. ……………………18分
不存在“均值”. ……………………18分 存在唯一的“均值”.这时函数
存在唯一的“均值”.这时函数 的均值为区间I两端点的算术平均数; ……………………13分
的均值为区间I两端点的算术平均数; ……………………13分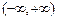 时,函数
时,函数 存在无数多个“均值”.这时任意实数均为函数
存在无数多个“均值”.这时任意实数均为函数 的“均值”; ……………………16分
的“均值”; ……………………16分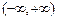 之外的其它区间时,函数
之外的其它区间时,函数 不存在“均值”. ……………………18分)
不存在“均值”. ……………………18分)


科目:高中数学 来源:不详 题型:单选题
 B.
B.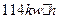 C.
C.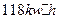 D.
D.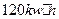
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的图像大致是 ( )
的图像大致是 ( )
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
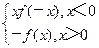 ,则{x|F(x)>0}=
,则{x|F(x)>0}=| A.{x|x<-3,或0<x<2,或x>3} |
| B.{x|x<-3,或-1<x<0,或0<x<1,或x>3} |
| C.{x|-3<x<-1,或1<x<3} |
| D.{x|x<-3,或0<x<1,或1<x<2,或2<x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com