
分析 (1)当a=0时求导可知f′(x)=ex-$\frac{b}{{e}^{x}}$,分b≤0与b>0两种情况讨论即可;
(2)通过分离参数可知条件等价于a<$\frac{{e}^{x}-{e}^{-x}}{2sinx}$恒成立,进而记g(x)=$\frac{{e}^{x}-{e}^{-x}}{2sinx}$,问题转化为求g(x)在(0,π)上的最小值问题,通过二次求导,结合洛必达法则计算可得结论.
解答 解:(1)当a=0时,f(x)=ex+be-x,f′(x)=ex-$\frac{b}{{e}^{x}}$,
当b≤0时,f′(x)>0恒成立,即此时函数f(x)的单调递增区间为(-∞,+∞);
当b>0时,令f′(x)=0,解得:x=$\frac{1}{2}$lnb,
当x<$\frac{1}{2}$lnb时f′(x)<0恒成立,x>$\frac{1}{2}$lnb时f′(x)>0,
∴此时函数f(x)的单调递减区间为(-∞,$\frac{1}{2}$lnb);函数f(x)的单调递增区间为($\frac{1}{2}$lnb,+∞);
(2)当b=-1时,函数f(x)=ex-e-x-2asinx,
又∵当x∈(0,π)时sinx>0,
∴f(x)>0对任意x∈(0,π)恒成立等价于a<$\frac{{e}^{x}-{e}^{-x}}{2sinx}$恒成立,
记g(x)=$\frac{{e}^{x}-{e}^{-x}}{2sinx}$,其中0<x<π,则g′(x)=$\frac{{e}^{x}(sinx-cosx)+{e}^{-x}(sinx+cosx)}{2si{n}^{2}x}$,
令h(x)=ex(sinx-cosx)+e-x(sinx+cosx),则h′(x)=2(ex-e-x)sinx>0,
∴h(x)在(0,π)上单调递增,h(x)>h(0)=0,
∴g′(x)>0恒成立,从而g(x)在(0,π)上单调递增,g(x)>g(0),
由洛必达法则可知,g(0)=$\frac{\underset{lim}{x→0}({e}^{x}-{e}^{-x})′}{\underset{lim}{x→0}(2sinx)′}$=$\frac{\underset{lim}{x→0}({e}^{x}+{e}^{-x})}{\underset{lim}{x→0}2cosx}$=1,
∴a≤1,即a的取值范围是(-∞,1].
点评 本题考查利用导数研究函数的单调性与不等式恒成立问题,涉及分类讨论的思想及分离参数法等技巧,涉及罗比达法则等知识,注意解题方法的积累,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 命题“如果p2+q2=2,则p+q≤2”的否命题是“如果p+q>2,则p2+q2≠2” | |
| B. | 命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∨q为假 | |
| C. | “若am2<bm2,则a<b”的逆命题为真命题 | |
| D. | 若${(\sqrt{x}-\frac{1}{{2\root{3}{x}}})^n}$的展开式中第四项为常数项,则n=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢户外活动 | 不喜欢户外活动 | 合计 | |
| 男性 | 20 | 5 | 25 |
| 女性 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
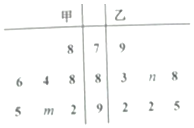 甲、乙两名同学在高一上学期7次物理考试成绩的茎叶图如图所示,其中甲成绩的平均数是88,乙学生的成绩中位数是89,则n-m的值是( )
甲、乙两名同学在高一上学期7次物理考试成绩的茎叶图如图所示,其中甲成绩的平均数是88,乙学生的成绩中位数是89,则n-m的值是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${log_{0.7}}6<{0.7^6}<{6^{0.7}}$ | B. | 0.76<60.7<log0.76 | ||
| C. | ${log_{0.7}}6<{6^{0.7}}<{0.7^6}$ | D. | ${0.7^6}<{log_{0.7}}6<{6^{0.7}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| B. | ①分层抽样,②系统抽样,③简单随机抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①简单随机抽样,②分层抽样,③系统抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 赞成“自助游” | 不赞成“自助游” | 合计 | |
| 男性 | 30 | ||
| 女性 | 10 | ||
| 合计 | 100 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com