练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    两两相交的四条直线确定平面的个数最多的是____个．


    1. A.
      4
    2. B.
      5
    3. C.
      6
    4. D.
      8
    C
    分析：充分利用好现成的几何体模型四面体即可很好地解决问题，四面体的四条棱正是两两相交的四条直线，它们确定平面的个数最多．
    解答：解：如四棱锥的四个侧面，
    C42=6个．
    故选C
    点评：本题主要考查了空间中直线与平面之间的位置关系，考查空间想象能力、运算能力和推理论证能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    如图（1），三棱锥P′-A′BC′中，P′A′⊥平面A′BC′，△A′BC′是正三角形，E是P′C′的中点；如图（2），PA⊥平面ACD，∠ACD=90°，∠DAC=30°．
    若△P′A′C′≌△PAC，现将两个三棱锥拼接成四棱锥P-ABCD，使得面△P′A′C′与面PAC完全重合．解答下列问题：
    （1）图（1）中，在边P′B上是否存在点F，使得FE∥平面A′BC′？若存在，说出F点位置；若不存在，说明理由；
    （2）在四棱锥P-ABCD中，已知数学公式．
    ①求证：CD⊥AE；
    ②求棱锥E-ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    在数学中“所有”一词，叫做全称量词，用符号“?”表示；“存在”一词，叫做存在量词，用符号“?”表示．
    设数学公式．
    ①?x0∈[2，+∞），使f（x0）=m成立，则实数m的取值范围为________；
    ②若?x1∈[2，+∞），?x2∈[2，+∞）使得f（x1）=g（x2），则实数a的取值范围为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    曲线y=x3在点（1，1）切线方程为 ________．

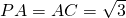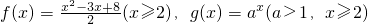    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某桶装水经营部每天的房租、人员工资等固定成本为200元，每桶水的进价为4元，销售单价与日均销售量的关系如下表所示：
    销售单价（元）567891011
    日均销售量（桶）480440400360320280240
    请根据以上数据作出分析，这个经营部怎样定价才能获得最大利润？请说明理由．（▲注：最后定价只能取整数元）

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设抛物线的焦点为F（-2，0），则抛物线的标准方程是


    1. A.
      y2=-8x
    2. B.
      x2=-8y
    3. C.
      y2=-4x
    4. D.
      x2=-4y

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    i是虚数单位，即i2=-1则1+C61i+C62i2+C63i3+C64i4+C65i5+C66i6=


    1. A.
      8i
    2. B.
      -8i
    3. C.
      8
    4. D.
      -16+16i

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
    年份200x（年）01234
    人口数y（十）万5781119
    （1）请画出上表数据的散点图；
    （2）请根据上表提供的数据，求出Y关于x的线性回归方程Y=bx+a；
    （3）据此估计2005年该城市人口总数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f（x）=lnx，g（x）=数学公式ax2-（a-1）x，（a∈R）．
    （Ⅰ）已知函数y=g（x）的零点至少有一个在原点右侧，求实数a的范围．
    （Ⅱ）记函数y=F（x）的图象为曲线C．设点A（x1，y1），B（x2，y2）是曲线C上的不同两点．如果在曲线C上存在点M（x0，y0），使得：①x0=数学公式；②曲线C在点M处的切线平行于直线AB，则称函数f（x）=存在“中值相依切线”．
    试问：函数G（x）=f（x）-g（x）（a∈R且a≠0）是否存在“中值相依切线”，请说明理由．

    查看答案和解析>>

    同步练习册答案