
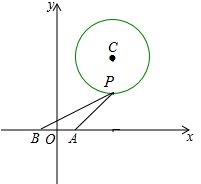
 如图,在平面直角坐标系内,已知A(1,0),B(-1,0)两点,且圆C的方程为x2+y2-6x-8y+21=0,点P为圆C上的动点.
如图,在平面直角坐标系内,已知A(1,0),B(-1,0)两点,且圆C的方程为x2+y2-6x-8y+21=0,点P为圆C上的动点.分析 (1)分类讨论,利用点到直线的距离等于半径,即可求过点A的圆的切线的方程;
(2)设P(x,y),利用两点间的距离公式表示出|AP|,|BP|,代入所求式子中化简,整理后得出所求式子最大即为|OP|最大,而P为圆上的点,连接OC延长与圆的交点即为此时的P点,(|OP|)max=|OC|+r,求出|OP|的最大值,即可确定出所求式子的最大值.
解答 解:(1)当k存在时,设过点A切线的方程为y=k(x-1),
∵圆心坐标为(3,4),半径r=2,∴$\frac{|3k-4-k|}{{\sqrt{1+{k^2}}}}=2$,
解得$k=\frac{3}{4}$,
∴所求的切线方程为3x-4y-3=0;…(3分)
当k不存在时方程x=1也满足;
综上所述,所求的直线方程为:3x-4y-3=0或x=1…(4分)
(2)设点P(x,y),则由两点之间的距离公式知|AP|2+|BP|2=2(x2+y2)+2=2|OP|2+2,
要|AP|2+|BP|2取得最大值只要使|OP|2最大即可,…(6分)
又P为圆上的点,所以${(|OP|)_{max}}=|OC|+r=\sqrt{{3^2}+{4^2}}+2=7$,
∴(|AP|2+|BP|2)max=2×72+2=100,…(9分)
此时直线$OC:y=\frac{4}{3}x$,由$\left\{{\begin{array}{l}{y=\frac{4}{3}x}\\{{x^2}+{y^2}-6x-8y+21=0}\end{array}}\right.$解得$\left\{{\begin{array}{l}{x=\frac{9}{5}}\\{y=\frac{12}{5}}\end{array}}\right.$(舍去)或$\left\{\begin{array}{l}{x=\frac{21}{5}}\\{y=\frac{28}{5}}\end{array}\right.$,
∴点P的坐标为($\frac{21}{5}$,$\frac{28}{5}$)…(12分)
点评 此题考查了直线与圆的位置关系,涉及的知识有:两点间的距离公式,圆的标准方程,坐标与图形性质,熟练掌握公式是解本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(-1,1) | B. | $\overrightarrow{a}$=(-1,1),$\overrightarrow{b}$=(2,-2) | C. | $\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(2,-2) | D. | $\overrightarrow{a}$=(1,-1),$\overrightarrow{b}$=(0,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
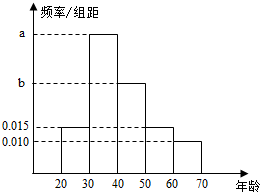 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com