
【题目】已知坐标平面上的凸四边形 ABCD 满足 ![]() =(1,
=(1, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,1),则凸四边形ABCD的面积为;
,1),则凸四边形ABCD的面积为; ![]()
![]() 的取值范围是 .
的取值范围是 .
【答案】2;[﹣2,0)
【解析】解:∵凸四边形 ABCD 满足 ![]() =(1,
=(1, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,1),
,1),
∴ ![]() =0,且AC|=2,BD=2,
=0,且AC|=2,BD=2,
∴AC=BD,AC⊥BD,
∴凸四边形ABCD的面积为 ![]() =
= ![]() =2;
=2;
设AC与BD交点为O,OC=x,OD=y,则AO=2﹣x,BO=2﹣y; ![]()
![]() =(
=( ![]() )(
)( ![]() )=
)= ![]()
=x(x﹣2)+y(y﹣2)=(x﹣1)2+(y﹣1)2﹣2,(0<x,y<2);
∴当x=y=1时, ![]()
![]() =﹣2为最小值,
=﹣2为最小值,
当x→0或1,y→0或1时, ![]()
![]() 接近最大值0,
接近最大值0,
∴ ![]()
![]() 的取值范围是[﹣2,0).
的取值范围是[﹣2,0).
故答案为:2;[﹣2,0).

根据向量的模的计算和向量的坐标运算得到四边形ABCD为对角线垂直且相等的四边形,问题得以解决.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点. (Ⅰ)证明:PB∥平面AEC;
(Ⅱ)若底面ABCD为正方形, ![]() ,求二面角C﹣AF﹣D大小.
,求二面角C﹣AF﹣D大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)在定义域[-1,1]上既是奇函数,又是减函数.
(1)求证:对任意x1,x2∈[-1,1],有[f(x1)+f(x2)]·(x1+x2)≤0;
(2)若f(1-a)+f(1-a2)<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD的中点.
的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD的中点.
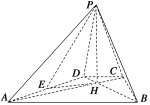
(1)证明:PE⊥BC;
(2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=asinx﹣bcosx(a,b为常数,a≠0,x∈R)在x= ![]() 处取得最小值,则函数g(x)=f(
处取得最小值,则函数g(x)=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函数且它的图象关于点(π,0)对称
B.奇函数且它的图象关于点(π,0)对称
C.奇函数且它的图象关于点( ![]() ,0)对称
,0)对称
D.偶函数且它的图象关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的可导函数f(x)满足f(x)﹣f(﹣x)=2x3 , 当x∈(﹣∞,0]时f'(x)<3x2 , 实数a满足f(1﹣a)﹣f(a)≥﹣2a3+3a2﹣3a+1,则a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:他们研究过图(1)中的1,3,6,10,…,由于这些数能够表示成三角形,所以将其称为三角形数;类似地,称图(2)中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )


A. 289 B. 1 024
C. 1 225 D. 1 378
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com