
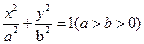 过点
过点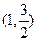 ,且长轴长等于4.
,且长轴长等于4.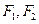 是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若
是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若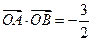 ,求
,求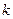 的值.
的值.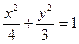

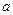 =4,得a=2, -------------------------1分
=4,得a=2, -------------------------1分 点
点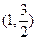 在椭圆上,
在椭圆上, ----------3分
----------3分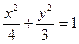 -------------------------------5分
-------------------------------5分 ---------------6分
---------------6分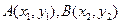 ,
,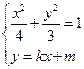 消去
消去 ,整理得
,整理得 ------7分
------7分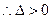 -------------------------8分
-------------------------8分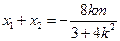
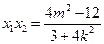 --------------------------------------9分
--------------------------------------9分 =
=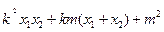
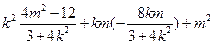 =
= -------------------10分
-------------------10分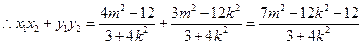 ----------------------11分
----------------------11分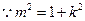
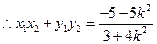 ---
--- -----------------12分
-----------------12分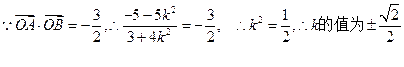 -------14分
-------14分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
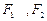 分别是椭圆C:
分别是椭圆C: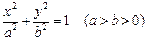 的左右焦点,
的左右焦点,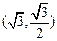 到
到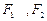 两点距离之和等于4,写出椭圆C的方程和焦点坐标。
两点距离之和等于4,写出椭圆C的方程和焦点坐标。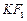 的中点B的轨迹方程。
的中点B的轨迹方程。 )设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为
)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为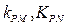 试探究
试探究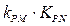 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com