
【题目】探究函数![]() 的图象与性质.
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并已画出了函数图象的一部分,请你画出该图象的另一部分;

(3)结合函数的图象,写出该函数的一条性质:_________;
(4)若关于x的方程![]() 有2个实数根,则t的取值范围是______.
有2个实数根,则t的取值范围是______.
科目:高中数学 来源: 题型:
【题目】若AC⊥BC,AC=BC=1,点P是△ABC内一点,则![]() 的取值范围是( )
的取值范围是( )
A. (﹣![]() ,0) B. (0,
,0) B. (0,![]() ) C. (﹣
) C. (﹣![]() ,
,![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数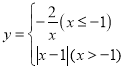 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
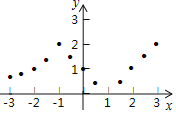
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”是我国数学史上的一个伟大成就,是二项式系数在三角形中的一种几何排列.如图所示,去除所有为1的项,依此构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前56项和为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.
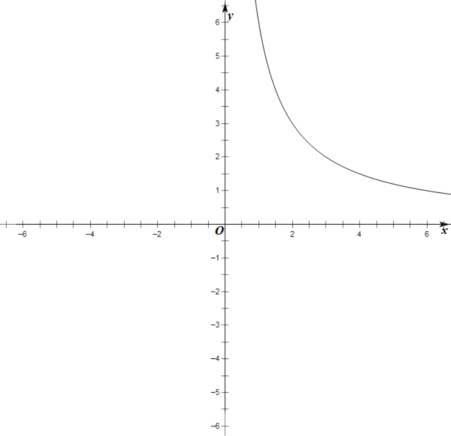
(1)自变量![]() 的取值范围是除
的取值范围是除![]() 外的全体实数,
外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() _________;
_________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出一条函数性质;
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________;
的实数根的情况是________;
②方程![]() 有_______个实数根;
有_______个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一容量为50的样本,数据的分组以及各组的频数如下:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9;[21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),5;[30.5,33.5],4.
(1)列出样本的频率分布表.
(2)画出频率分布直方图.
(3)根据频率分布表,估计数据落在[15.5,24.5)内的可能性约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解校园安全教育系列活动的成效,对全市高中生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化,现随机抽取部分高中生的答卷,统计结果如下,对应的频率分布直方图如图所示.
等级 | 不合格 | 合格 | ||
得分 | [20,40) | [40,60) | [60,80) | [80,100) |
频数 | 12 |
| 48 | 24 |
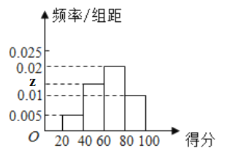
(1)求![]() 、
、![]() 的值;
的值;
(2)估计该市高中生测试成绩评定等级为“合格”的概率;
(3)在抽取的答卷中,用分层抽样的方法,从评定等级为“合格”和“不合格”的答卷中抽取5份,再从这5份答卷中任取2份,求恰有1份评定等级为“不合格”的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com