
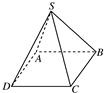
 如图,四棱锥S-ABCD的所有棱长均为1米,一只小虫从S点出发沿四棱锥爬行,若在每顶点处选择不同的棱都是等可能的.设小虫爬行n米后恰回到S点的概率为Pn(n≥2,n∈N).
如图,四棱锥S-ABCD的所有棱长均为1米,一只小虫从S点出发沿四棱锥爬行,若在每顶点处选择不同的棱都是等可能的.设小虫爬行n米后恰回到S点的概率为Pn(n≥2,n∈N).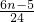 (n≥2,n∈N).
(n≥2,n∈N). =
= ;
; ×2=
×2= ,
, ×4=
×4= .
. ×(1-Pn)=Pn+1,即3Pn+1+Pn=1(n≥2,n∈N).
×(1-Pn)=Pn+1,即3Pn+1+Pn=1(n≥2,n∈N). =-
=-
 ,
, +
+
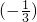 n-2(n≥2,n∈N).
n-2(n≥2,n∈N).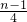 +
+
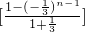
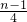 +
+
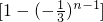
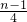 +
+ ×
× +
+
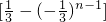 >
>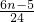 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com