
 与
与 不共线,若存在非零实数x,y,使得
不共线,若存在非零实数x,y,使得 =
= +2x
+2x ,
, =-y
=-y +2(2-x2)
+2(2-x2) .
. =
= 时,求x,y的值;
时,求x,y的值; =(
=(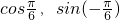 ),
), =(
=(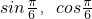 ),且
),且 ⊥
⊥ ,试求函数y=f(x)的表达式.
,试求函数y=f(x)的表达式.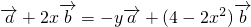 ,
, +(2x-4+2x2)
+(2x-4+2x2) =
= ,
, 与
与 不共线,
不共线,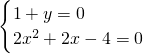 ,解得y=-1,x=1或x=-2.
,解得y=-1,x=1或x=-2. =cos
=cos sin
sin +sin(-
+sin(- )cos
)cos =0,∴
=0,∴
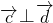 ,∴
,∴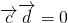 ,又由条件可知,
,又由条件可知,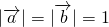
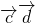 =(
=(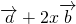 )•[
)•[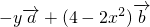 ]
] -2xy
-2xy +(4-2x2)
+(4-2x2) +2x(4-2x2)
+2x(4-2x2)
 +(2x-4+2x2)
+(2x-4+2x2) =
= ,∵向量
,∵向量 与
与 不共线,故
不共线,故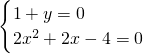 ,解之即可;
,解之即可;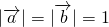 ,
,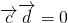 ,
,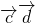 =(
=(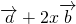 )•[
)•[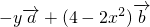 ]=-y
]=-y -2xy
-2xy +(4-2x2)
+(4-2x2) +2x(4-2x2)
+2x(4-2x2) =-y+2x(4-2x2)=0,移项可得y的解析式.
=-y+2x(4-2x2)=0,移项可得y的解析式.

 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
| a |
| b |
| c |
| b |
| c |
| d |
| a |
| b |
| c |
| d |
| a |
| a |
| MP |
| MA |
| MB |
| OP |
| OA |
| OB |
| OC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| m |
| n |
| m |
| n |
| a |
| b |
| c |
| m |
| n |
| m |
| n |
| m |
| n |
| a |
| b |
| c |
| m |
| n |
| m |
| n |
| m |
| n |
| a |
| b |
| c |
| m |
| n |
| m |
| n |
| m |
| a |
| n |
| b |
| c |
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| 0 |
| b |
| a |
| λ | 2 1 |
| +λ | 2 2 |
| a |
| b |
| 0 |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com